Економіка грошей, банківської справи і фінансових ринків - Мишкін Ф.С. - Підсумки.

Для розрахунку доходу на момент погашення для купонної облігації дотримуємося цієї ж стратегії, яка використовувалася для позички з незмінним платежем, тобто зрівнюємо нинішню вартість облігації з її поточною вартістю. Оскільки купонна облігація передбачає більше ніж один платіж, то поточна вартість розраховується як сума поточних вартостей всіх купонних платежів плюс поточна вартість кінцевого платежу номінальної вартості облігації.

Поточну вартість облігації номінальною вартістю 1000 дол. з десятирічним строком погашення і щорічним купонним доходом 100 дол. (10 %-на купонна ставка) можна обчислити таким чином. В кінці

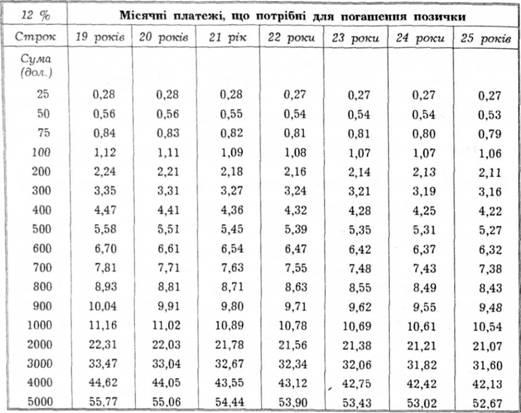
Графік 4.1. Таблиця по заставних платежах. Позичка з фіксованим платежем, процентною ставкою 12 % і строком виплат 25 років передбачатиме, як видно з таблиці, місячний платіж у 10,54 дол. (126 дол. на рік).

першого року має місце купонний платіж (доход) у сумі 100 дол. з РУ, що дорівнює 100 дол./(1 + г); наприкінці другого року має місце наступний купонний платіж у сумі 100 дол. з РУ, що дорівнює 100 дол./(1 + і)2 і т. д., аж поки не наступить строк погашення з купонним платежем 100 дол. і з РУ, що дорівнює 100 дол./(1 + і)10 плюс погашення номінальної вартості облігації 1000 дол. з РУ, що дорівнює 1000 дол./(1 + і)10. Встановлюючи нинішню вартість облігації (її поточна ціна, що позначена через Р^) рівною сумі поточних вартостей всіх платежів для цієї облігації, запишемо:

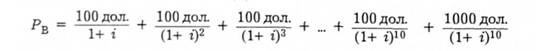
Загальніше для будь-якої купонної облігації маємо 1:

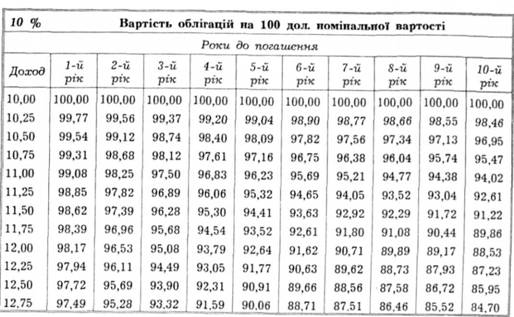
Графік 4.2. Таблиця облігацій. Для 10-річної облігації з 10 %-ною купонною ставкою ця таблиця показує, що доход на момент погашення 11,75 % відповідає ціні 89,86 дол. на 100 дол. номінальної вартості (тобто облігація з номінальною вартістю 1000 дол. продається приблизно за 900 дол).

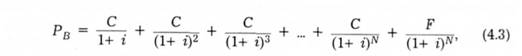
де С - щорічний купонний платіж (доход), Р - номінальна вартість облігації, N - роки до погашення облігації, Рв - ціна купонної облігації. У рівнянні (4.3) купонний платіж, номінальна вартість, роки до погашення і ціна облігації є відомими величинами, і тільки доход на момент погашення невідомий Отже, ми можемо розв'язати це рівняння для доходу на момент погашення, і1. Як і у випадку з позичкою з незмінним платежем, цей розрахунок не є легким, тому була створена таблиця облігацій (графік 4.2), що подає доход на момент погашення для облігації з певною ставкою купона, терміном погашення та ціною. В ряд ділових кишенькових калькуляторів закладено програми, що дозволяють розв'язувати це рівняння 2.

Погляньмо на декілька прикладів визначення доходу на момент погашення по 10 %-ній купонній облігації, строк погашення якої виходить через десять років. Якщо купівельна ціна облігації становить 1000 дол, тоді або через використання кишенькового калькулятора із закладеною у нього програмою, або дивлячись у таблицю облігацій, ми знайдемо, що доход на момент погашення є 10 %. Якщо ціна облігації дорівнює 900 дол., тоді знайдемо, що доход на момент погашення є 11,75 %. Таблиця 4.1 показує, що доход на момент погашення обчислюється для декількох різних курсів облігацій.

ТАБЛИЦЯ 4.1. Доход на момент погашення по облігації з 10 %-ною купонною ставкою; строк погашення облігації 10 років (номінальна вартість дорівнює 1000 дол.).

Три цікаві висновки випливають із таблиці 4.1:

(1) Якщо купонна облігація оцінюється за номінальною вартістю, або номіналом, то доход на момент погашення дорівнює купонній ставці.

(2) Ціна купонної облігації і доход на момент погашення перебувають в оберненій залежності, тобто, коли доход на момент погашення зростає, то ціна облігації падає. Якщо доход на момент погашення падає, то ціна облігації зростає.

(3) Доход на момент погашення є більшим за купонну ставку, коли ціна облігації є нижчою за номінальну вартість.

Ці три обставини правильні для будь-якої купонної облігації, як це випливає з розрахунку доходу на момент погашення. Коли ви покладете 1000 дол на банківський рахунок із ставкою 10 %, то ви можете щорічно вилучати 100 дол і все ж залишиться 1000 дол в кінці десятого року. Щось подібне відбувається з купівлею облігації на 1000 дол з 10 %-ною купонною ставкою, що аналізується в таблиці 4.1. По цій облігації виплачується купонний доход у 100 дол щорічно, а тоді облігація викуповується за 1000 дол. наприкінці десятого року. Якщо облігація викуповується за номінальною вартістю 1000 дол, то її доход на момент погашення повинен дорівнювати ставці 10 %, яка також дорівнює купонній ставці 10 %. Таке міркування, що застосовне до будь-якої купонної облігації, показує, що коли купонна облігація купується за її номінальною вартістю, то доход на момент погашення і купонна ставка повинні бути рівними.

Просто показати, що ціна облігації і доход на момент погашення перебувають в оберненій залежності Коли і, доход на момент погашення, зростає, то всі знаменники у формулі ціни облігації повинні обов'язково зростати. Отже, зростання процентної ставки, яка виміряна на момент погашення, означає, що ціна облігації повинна впасти. Інший спосіб пояснення, чому ціна облігації падає, коли процент зростає, полягає в тому, що вища процентна ставка означає, що майбутні купонні доходи і кінцевий доход знижуються, коли дисконтуються у поточну вартість. Звідси, ціна облігації повинна бути нижчою. Існує спеціальний, вартий уваги, випадок купонної облігації, бо доход на момент погашення по цій облігації обчислюється особливо легко. Ця облігація називається консоль. Консоль - це рентна облігація, яка не має строку погашення, не має платежів по основній сумі боргу і завжди дає незмінні купонні платежі (С).

Консолі вперше продані міністерством фінансів Великобританії під час наполеонівських війн, і їх все ще продають і купують сьогодні. Проте вони є рідкісними на ринку капіталів у США. Формула рівняння (4.3) для ціни консоля (Рс) спрощується до такої:

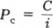
(4.4)

Одна важлива риса консолів полягає в тому, що ви можете одразу бачити, що коли і зростає, то ціна облігації падає. Наприклад, якщо консоль дає 100 дол. на рік, а процентна ставка 10 %, то ціна цієї облігації становитиме 1000 дол = 100 дол./ОДО. Якщо ставка зросте до 20 %, то ціна консоля впаде до 500 дол 100 дол/0,20. Цю формулу можна також записати таким чином:

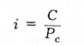
Ми бачимо, що також легко обчислити доход на момент погашення для консоля (незважаючи на те, що він ніколи не погашається). Наприклад, для консоля, що приносить 100 дол. щорічно і з ціною 2000 дол., доход на момент погашення легко обчислюється і становить 5 % (= 100 дол/2000 дол).

Дисконтна облігація.

Розрахунок доходу на момент погашення для дисконтної облігації такий же, як і для простої позички. Давайте розглянемо дисконтну облігацію, приміром, однорічний вексель Державної скарбниці США, який викуповується за номінальною вартістю 1000 дол. через один рік. Якщо поточна купівельна ціна цього векселя становить 900 дол., то, прирівнюючи цю ціну до поточної вартості 1000 дол, яка отримана через рік, застосуємо рівняння (4.1) і отримаємо:

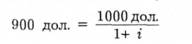
Знаходимо і:

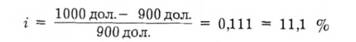
Загальніше для однорічної дисконтної облігації доход на момент погашення можна записати:

де F - номінальна вартість дисконтної облігації, Рй - поточна ціна дисконтної облігації.

Іншими словами, доход на момент погашення дорівнює зростанню ціни протягом року - Ргі), що поділене на вихідну ціну (Рй).

Важлива риса цього рівняння полягає в тому, що воно показує для дисконтної облігації: доход на момент погашення перебуває в оберненій залежності від поточної ціни облігації. Це той самий висновок, якого ми дійшли для купонної облігації. Наприклад, рівняння (4.6), яке подане вище, показує, що зростання ціни облігації з 900 дол. до 950 дол. означає, що облігація матиме менше зростання ціни протягом її життя Тому доход на момент погашення впаде з 11,1 до 5,3 %. Так само падіння доходу на момент погашення означає, що ціна дисконтної облігації зросла.

Підсумки.

Поняття поточної вартості означає, що один долар в майбутньому не є таким цінним, як один долар сьогодні, бо ви можете заробити процент на нього. Зокрема, один долар, що одержаний через п років, вартий тільки 1 дол./(1 + г)п сьогодні Поточна вартість майбутніх платежів по борговому інструменту дорівнює сумі поточних вартостей кожного з майбутніх платежів. Доход на момент погашення як показник є процентною ставкою, що дорівнює відношенню поточної вартості від майбутніх платежів по борговому інструменту до її вартості сьогодні Оскільки методи обчислення доходу на момент погашення ґрунтуються на надійних економічних принципах, то він є вимірником, котрий економісти розглядають як такий, що найточніше описує процентну ставку.

Наші обчислення доходу на момент погашення для різних видів облігацій виявляють важливу обставину: поточні ціни облігацій і процентні ставки перебувають в оберненій залежності. Коли процентна ставка зростає, то ціна облігації падає, і навпаки.