Економічна теорія управління фірмою - Іванова Н.Ю - 1.2. Прийняття рішень за умов різних станів середовища

Проблема прийняття рішень існує, коли за певним станом зовнішнього середовища із декількох альтернатив має бути обрана найкраща.

Відповідно до цього проблема прийняття рішень складається з таких елементів:

- стану зовнішнього середовища;

- наявності альтернатив;

- мети.

Стан зовнішнього середовища - це реальний стан справ, який не залежить від особи, що приймає рішення.

Альтернатива - це один із можливих, незалежних від інших засіб дії задля досягнення мети.

Мета - це вираження бажаних станів, що мають виникнути як результат прийняття рішення.

Оскільки рішення приймаються особою, то вони залежать від знань цієї особи. Стан знань особи, яка приймає рішення, класифікують як стан визначеності, ризику і невизначеності.

Визначеність - це такий стан знань, коли особа, що приймає рішення, заздалегідь знає конкретний результат для кожної альтернативи.

Ризик - це такий стан знань, коли відомі один або декілька результатів для кожної альтернативи і ймовірність реалізації кожного результату.

Невизначеність - це такий стан знань, коли одна або декілька альтернатив мають декілька можливих результатів, ймовірність яких або невідома, або не має сенсу.

Прийняття рішень в умовах визначеності полягає у пошуку або максимізації вигоди (дохід, прибуток, корисність), або мінімізації витрат. Такий пошук має назву оптимізаційного аналізу. Зазвичай використовують такі методи оптимізації:

- граничний аналіз;

- лінійне програмування;

- прирістний аналіз прибутку;

- аналіз суб'єктивної корисності.

Граничний аналіз використовує концепції граничних витрат MC (Marginal Cost) і граничного доходу MR (Marginal Revenue). Він передбачає, що менеджер знає вигляд функції доходу і функції витрат і не враховує обмеження на наявність ресурсів, умови їх використання, а також обмеження на обсяги виробництва.

Слід зазначити, що граничний аналіз має справу із змінами значень пов'язаних, але незмінних функцій.

Лінійне програмування - це вид математичного моделювання, який використовується для пошуку оптимального варіанту розподілу обмежених ресурсів між конкуруючими роботами. Задачею лінійного програмування буде будь-яка економічна задача, що пов'язана із оптимізацією лінійної цільової функції (наприклад, функції прибутку або витрат) і комплексу лінійних нерівностей (наприклад, обмежень на робочу силу, матеріальні ресурси і т.ін.)

Концепція прирістного аналізу прибутку охоплює зміни як значень функції, так і самих функцій. Основне правило полягає в тому, щоб прийняти пропозицію, яка сприяє зростанню прибутку.

Прирістні рішення відносяться до короткострокових, оскільки в них розглядаються лише змінні, які підлягають змінам. Постійні складові витрат не розглядаються.

Приклад. Обсяг виробництва - 100 000 одиниць, ціна - 24 грн, середні змінні витрати - 14 грн, постійні витрати - 600 000 грн.

У фірми з'являється можливість укласти контракт на додатковий продаж 25 000 од. за ціною 18 грн. Для виготовлення додаткових одиниць виробник має працювати понаднормово, що потребує додаткових середніх змінних витрат 2 грн.

Чи доцільно укладати такий контракт?

Якщо менеджер буде приймати рішення, виходячи із середньої вартості одиниці продукції, то контракт не буде укладено. Але якщо розраховувати прирістні витрати, то прирістна вартість 25 000 од. складе 16 грн за одиницю, а прирістний дохід складе 18 грн, тобто прирістний прибуток за одиницю продукції становить 2 грн, а відповідно сукупний прибуток - 50 000 грн (2 ^х 25 000). Отже, укладати контракт доцільно, оскільки виробництво додаткових одиниць продукції не потребує додаткових постійних витрат, а постійні витрати в 600 000 грн покриваються за рахунок доходу, який отримує фірма від старого обсягу виробництва. Аналіз суб'єктивної корисності здійснюється двома методами:

- лексикографічного порядку;

- зважування цілей.

За методом лексикографічного порядку цілі впорядковуються відповідно до їх пріоритетності. Якщо одна альтернатива задовольняє найважливішу ціль краще, ніж інші, то обирається ця альтернатива. Наступні за ступенем важливості цілі є суттєвими лише в тому випадку, якщо як мінімум дві альтернативи рівнозначущі відносно найважливішої цілі. Якщо ж перевірка альтернатив на основі другої за важливістю цілі не дає оптимуму, то порівняння продовжується доти, доки одна з альтернатив не переважить інші.

За методом зважування цілей враховуються всі цілі відповідно до їх вагомості, яка визначається суб'єктивно. Результати окремих альтернатив помножуються на відповідні значення важливості цілі, а потім обирається альтернатива з найвищим значенням суми.

Приклади застосування:

1. Вибір місця розташування фірми

S_i - місце розташування фірми. Результати вибору (а.) визначаються за допомогою балів (від 0 до 10). Кращим є місце розташування S₂.

2. Вибір організаційно-правової форми господарювання

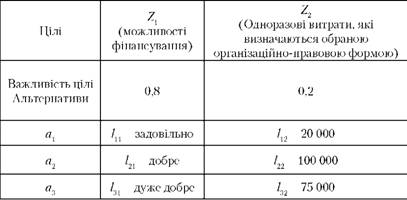
Виникає проблема визначення цільових значень альтернативних результатів.

Для цілі 2₂ результати наведені у кількісній формі і тому можна використовувати кардинальну шкалу цільових значень: результати оцінюються балами від 0 до 10:

Крім кардинальної шкали існують ординальна (для результатів встановлюються ранги значущості - 1 місце, 2 місце і т.д.), а також номінальна шкала (складається з двох оцінок (значення не досягнуто), 1 (значення досягнуто)).

В нашому випадку

а₁: 0,8x6 + 0,2x8 = 6,4;

а₂: 0,8x8 + 0,2x0 = 6,4;

а₃: 0,8x10 + 0,2x2,5 = 8,5 - найкраща.

В умовах визначеності, як правило, приймаються короткострокові рішення.

Однак практично всі довгострокові рішення приймаються в умовах ризику та невизначеності.

Існують наступні правила прийняття рішення в умовах ризику: Правило Байеса ( μ-принцип);

- (μ, 5) - принцип;

- принцип Бернуллі.

Яке рішення обере менеджер, головним чином залежить від його схильності до ризику. Отже важливим є урахування схильності до ризику особи, яка приймає рішення.

Якщо рішення приймається в умовах невизначеності, то використовують такі правила:

- правило шахшіи (критерій Вальда), за допомогою якого обирається стратегія, що забезпечує найкращий із найгірших результатів;

- правило шіишах (критерій Сейвіджа), дозволяє мінімізувати збитки в результаті прийняття неправильного рішення;

- а-критерій Гурвиці надає можливість звернути увагу на найгіршу і на найкращу віддачу від конкретної стратегії і визначити суб'єктивну імовірність для кожної з них;

- критерій Лапласа за яким, якщо імовірності явища невідомі, то вони мають бути прийняті рівними.