Інвестування - Гриньова В.М. - 3.1.3. Оцінка дохідності окремих видів фінансових активів

Видами доходу за будь-яким фінансовим активом є дохід від володіння та дохід від перепродажу фінансового активу на вторинному ринку. Дохід від володіння борговим зобов'язанням з плаваючою ставкою корегується ринком незалежно від того, існують чи не існують на вторинному ринку такі зобов'язання. Дохід від володіння борговим зобов'язанням із фіксованим купоном визначається ставкою купона, якщо це зобов'язання не перебуває в обігу на вторинному ринку і корегується ринковою ціною під час його перепродажу на ринку. При цьому очікуваний рівень доходу за зобов'язанням відповідає ринковій дохідності подібних зобов'язань.

Визначення ставки доходу від володіння фінансовим активом здійснюється з урахуванням часового чинника і ґрунтується на оцінці очікуваних грошових потоків за ним. Очікуваний рівень доходу від володіння борговим зобов'язанням розраховується на основі купонних виплат, номінальної вартості та часового періоду до погашення фінансового активу. Очікувана дохідність акції обчислюється, виходячи з певних припущень щодо обсягу очікуваних дивідендів. Оскільки майбутній обсяг дивідендних виплат залежить від багатьох чинників, навіть у стабільних умовах діяльності корпорації та дивідендної політики визначення очікуваної дохідності акцій є здебільшого досить складним завданням.

Дохідність операцій з купівлі-продажу фінансових активів на вторинному ринку, як правило, розраховують на основі короткострокових часових періодів (менш як рік) у вигляді річної процентної ставки. Так само визначають дохідність короткострокових фінансових активів.

Для визначення дохідності операцій з фінансовими активами на вторинному ринку використовують формулу

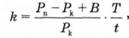
де Рn — ціна продажу чи погашення фінансового активу;

Рk — ціна купівлі фінансового активу на ринку;

В — процентні чи дивідендні виплати за період t;

Т — часова база (365 або 360 днів);

t — період володіння фінансовим активом.

Період володіння t фінансовим активом, як правило, менший від 1 року, оскільки спекулятивні операції проводяться переважно в короткостроковий період. Крім того, багато таких операцій здійснюються з інструментами грошового ринку, термін обігу яких менший за 1 рік, і які часто розміщуються на дисконтній основі.

Розглянемо три основні способи визначення ставки доходу за векселями та іншими дисконтними цінними паперами, які базуються на використанні формул простих і складних процентів. Ставку доходу, обчислену цими трьома способами, називають відповідно банківською дисконтною, купонно-еквівалентною та ефективною.

Банківську дисконтну ставку доходу k6 визначають за формулою

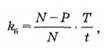
де N — номінальна вартість векселя;

Р — ринкова вартість векселя;

Т — часова база;

t — термін погашення векселя, днів.

Процентну ставку k також називають обліковою. Якщо банк вказує таку ставку, то за нею можна розрахувати суму Р, яка буде сплачена банком власнику векселя при його обліку, та дохід банку — дисконт D від обліку векселя. Отже, відповідно до формул (3.10)

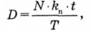
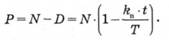
Дохідність операцій з обліку векселя, як і дохідність будь-якої операції з фінансовими активами на вторинному ринку, може бути розрахована на основі формули (3.11). Відповідний дохід називається купонно-еквівалентним доходом:

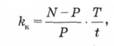
де N — визначає ціну продажу, або номінальну вартість боргового зобов'язання, за якою відбудеться погашення;

Р— поточна ринкова ціна зобов'язання.

За цією формулою (3.12) можна визначити дохідність операцій з купівлі-продажу чи купівлі з подальшим погашенням будь-якого дисконтного боргового зобов'язання.

Користуючись формулою (3.12), можна визначити, якою має бути ціна дисконтного зобов'язання на вторинному ринку, щоб забезпечити інвестору дохідність у розмірі k_к:

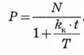
За цією формулою (3.13) та формулою (7.4) можна отримати залежність між банківсько-дисконтним і купонно-еквівалентним доходом:

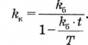
Чим менша кількість днів г до погашення векселя, тим менше відрізняються ставки k_к і k_б, незалежно від початкового терміну погашення векселя. У цілому ставка купонно-еквівалентного доходу k_к завжди перевищує ставку k_б.

Для того щоб зберігати реальну дохідність операцій на вторинному ринку на належному рівні в умовах інфляції потрібно визначити процентні ставки k_к і k_б з урахуванням відповідних рівнів інфляції. За рівня інфляції ї за період t для забезпечення реальної дохідності операцій обліку векселя на рівні, що визначається величиною k_к, треба номінальну вартість векселя N скорегувати на множник (1 + і). Використовуючи формулу (3.6), отримаємо

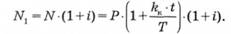
З іншого боку, скореговану величину N_l можна подати у вигляді

де k_к1 — ставка, що враховує інфляцію.

Порівнявши вирази (3.8) і (3.9) та здійснивши деякі перетворення, отримаємо

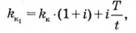
де k_к1 — номінальна купонно-еквівалентна ставка доходу, яка забезпечує інвестору реальну дохідність на рівні k за рівня інфляції і за період і.

Аналогічно можна визначити облікову ставку k_б1, що компенсує інфляційні витрати і забезпечує реальну дохідність, яка визначається обліковою ставкою:

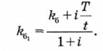
Крім банківсько-дисконтної та купонно-еквівалентної ставок доходу, у фінансових розрахунках для визначення дохідності дисконтних боргових зобов'язань використовують також ефективну ставку доходу, яка визначається за формулою

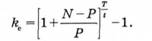
Ринкова вартість дисконтного зобов'язання, що забезпечує необхідний рівень ефективного доходу к k₀, розраховується на основі формули:

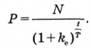
Класична інвестиційна теорія розглядає показник прибутковості за період володіння стосовно будь-якої інвестиції, у тому числі й цінних паперів. При цьому припускається, що будь-які виплати, отримані за період, були реінвестовані і використані для придбання цінних паперів за поточним ринковим курсом. Тоді прибутковість за період володіння (Д_пв), із врахуванням нарахувань доходу методом складних відсотків, має вигляд

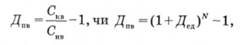
де Д_пв — еквівалентна одинична прибутковість за період володіння;

N — кількість одиничних проміжків за період володіння;

С_кв — вартість на кінець періоду володіння;

С_нв — вартість на початок періоду володіння.

Для того щоб одержати прибутковість за час володіння в розрахунку на один період використовують показник середньої геометричної прибутковості. На практиці найбільш придатний період володіння найчастіше настільки невизначений, як і прибутковість для певного періоду володіння. Проте таке припущення при ухваленні інвестиційного рішення дає змогу сфокусувати увагу на найбільш придатному в цій ситуації тимчасовому проміжку, одержати досить точний критерій і спростити розрахунки.

Обчислити прибутковість за період володіння методом екстраполяції не так уже й складно, проте спрогнозувати її непросто, з огляду на наявність великої кількості невизначеностей, пов'язаних як з виплатами за цінними паперами, так і з ситуацією, що змінюється на ринку. Тому очікувана прибутковість може бути обчислена як середньозважена можливих дохідностей за період володіння з використанням імовірностей як коефіцієнта.

Розглянемо склад прибутковості на прикладі акцій, зокрема зростання її курсової вартості за період і дивідендні виплати. Для простих акцій формула зростання має вигляд

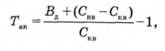
де Т_ак — прибутковість акції;

В_д — дивідендні виплати за акціями.

Дивідендна політика кожної компанії залежить від її прибутків і наявності коштів, при цьому дивіденди, що виплачуються за поточний рік, можуть бути вищі чи нижчі, ніж дивіденди, що виплачуються за попередній рік, а за окремі роки дивіденди можуть бути взагалі не виплачені.

З часом річний дивіденд за акцією може залишатися незмінним, може рівномірно збільшуватись досить швидко протягом декількох років, потім знову збільшуватися рівномірно. З огляду на все це, розрахунок ціни звичайних акцій вимагає обережного прогнозу майбутніх дивідендів, тому що ми припускаємо, що емітент буде існувати завжди, ціна звичайних акцій не залежить від того, скільки років інвестори планують володіти акціями.

Величину грошового потоку дивідендів визначають три фактори: річні дивіденди, темпи приросту дивідендів і ставка дисконту (необхідна ставка доходу). При цьому розглядається кілька випадків дивідендних виплат: постійні дивіденди; постійний приріст дивідендів (модель Гордона) і нерівномірні виплати дивідендів.

Якщо має місце постійний річний дивіденд В_д і необхідна ставка доходу k то ціна звичайних акцій Т_ак може бути визначена за допомогою дисконтування майбутніх дивідендів під k:

Така сама формула використовується і для оцінки привілейованих акцій, з тією різницею, що необхідна ставка прибутковості звичайних акцій, яка залежить від їхньої ризикованості відсутня, а в розрахунок береться ставка твердих дивідендних виплат.

Якщо щорічні темпи зростання дивідендів емітента є постійними, то для визначення прибутковості використовується формула Гордона:

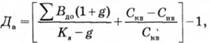
де В_до — останній виплачений дивіденд за акцію;

Д_а — очікувані дивіденди на акцію через рік;

К_s — необхідна ставка доходу;

g — темпи приросту дивідендів.

Протягом перших декількох років дивіденди фірми можуть значно збільшитися, потім темпи приросту нормалізовуються, стають стабільними. У цьому випадку постає питання, як оцінити акцію, коли дивіденди мають різні темпи приросту за окремі періоди. Ця проблема вирішується просто: якщо використовувати той самий принцип оцінки, що й у попередніх випадках, то ціна цінних паперів є теперішньою вартістю їхніх майбутніх доходів. Коли дивіденди збільшуються нерівномірно, то треба обчислити майбутні дивіденди окремо за кожен період, потім дисконтувати ці суми до теперішньої вартості і додати отримані результати:

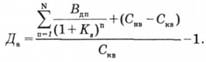
Оскільки власники привілейованих акцій регулярно одержують фіксовані дивіденди від емітентів, то їх можна розглядати як вічну ренту, і прибутковість таких акцій можна також визначити, дисконтуючи суму дивідендів за нескінченний період.

Вартість акцій, як і розмір акціонерного капіталу, може бути виражена у декількох вартісних характеристиках. Сумарна ринкова вартість усіх випущених акцій становить ринкову капіталізацію акціонерного товариства і слугує оцінкою вартості підприємства з позицій фондового ринку. Статутний фонд відповідно відображає лише частку вкладень у підприємство і не дає повного уявлення про його реальну вартість.

Однак й оцінка вартості підприємства за показником акціонерного капіталу ринкової капіталізації має ряд суттєвих недоліків. По-перше, цей показник може змінюватись залежно від загального стану ринку цінних паперів. По-друге, стосовно підприємства-банкрута курс акцій на ринку завжди буде падати значно нижче рівня реальної балансової вартості внаслідок панічного настрою інвесторів. По-третє, капіталізацію можна розрахувати тільки тоді, коли акції активно обертаються на фондовому ринку, а інвестор має доступ до котирувальної інформації, що для українського ринку швидше виняток, ніж правило.

В умовах відсутності інформації про ринкові коливання цін акцій або за наявності сумнівів у її вірогідності, можна рекомендувати використовувати розрахункові методи, маючи на увазі, що розрахункова вартість випущених акцій дорівнює оціночній вартості підприємства.

Розвиток фондових ринків розвинутих країн супроводжується підвищенням капіталізації компаній, зростанням курсової вартості їх акцій, значним поширенням цінних паперів. Забезпечення захисту прав акціонерів позитивно впливає на покращення інвестиційного клімату в регіоні чи в державі в цілому.

Зазначимо, що український фондовий ринок через його низьку капіталізацію, невідповідність міжнародним стандартам, нерозвиненість інфраструктурних елементів, слабку правову базу щодо захисту інтересів інвесторів має надзвичайно низький рівень інтеграції у світовий та європейський ринки капіталів. Однією з причин недостатньої ефективності вітчизняного фондового ринку, на думку фахівців, є значне розшарування кола інвесторів України. З одного боку, професіонали, а з іншого — значна кількість потенційних інвесторів майже необізнаних щодо понять фондового ринку та власних можливостей діяльності на ньому.

Визначимо певні орієнтири щодо ефективного вкладання коштів на фінансовому ринку.