Логіка - Дуцяк І.3. - Інструменти. Алгоритм виявлення правильності силогізму методом Джона Венна

Правильність силогізмів можна визначити за допомогою графічних методів, один з яких полягає у порівнянні діаграм Ейлера для засновків і для висновку. Цей метод значно простіший (не треба пам'ятати жодних правил). Крім того, він є універсальним, оскільки за його допомогою можна брати засновками довільні твердження, а не тільки ті чотири види тверджень, для яких чинна силогістика.

Інструменти. Алгоритм виявлення правильності силогізму:

1. Будують діаграму Ейлера для засновків.

2. Будують діаграму Ейлера для висновку.

3. Порівнюють діаграми, шляхом порівняння діаграм з'ясовують, чи відповідає діаграма висновку діаграмі засновків. Якщо нема повної відповідності між діаграмами відношення обсягів 5 і Р, зафіксованими у засновках, та діаграмами, зафіксованими у висновку, то вивід є необґрунтованим.

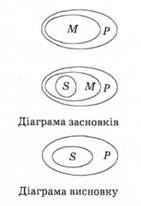
Приклад 1: обґрунтувати правильність (чи неправильність) силогістичного виводу, розміщеного праворуч, за допомогою діаграм Ейлера.

1. Будуємо діаграму відношень між обсягами термінів ссавці (М) і тварини (Р). Між цими іменами є відношення підпорядкованості. На цій самій діаграмі зображаємо також відношення між обсягами термінів ссавці і люди (5). Між цими іменами також відношення підпорядкованості. У підсумку отримуємо діаграму засновків.

2. Будуємо діаграму Ейлера для висновку. Між іменами люди і тварини є відношення підпорядкованості. Діаграма висновку, зображена під діаграмою засновків, - праворуч.

3. Зіставляємо діаграму висновку з діаграмою засновків і бачимо, що у висновках зафіксоване те саме відношення між обсягами імен, яке зафіксоване в засновках. Отже, вивід є правильним.

Приклад 2: обґрунтувати правильність (чи неправильність) силогістичного виводу, розміщеного праворуч, за допомогою діаграм Ейлера.

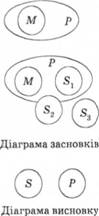
1. Будуємо діаграму відношень між обсягами термінів адвокати (М) і юристи (Р). Між зазначеними іменами є відношення підпорядкованості. На цій самій діаграмі зображаємо також відношення між обсягами термінів адвокати і прокурори (5). Між цими іменами є відношення несумісності. Однак коло, яким позначено прокурорів (в), перебуваючи за межами кола М, може бути в різних відношеннях з колом Рі 1) у відношенні несумісності (&); у відношенні перехрещеності (52); 3) у відношенні підпорядкованості (&3).

2. Будуємо діаграму Ейлера для висновку. Між іменами прокурори і юристи висновком зафіксоване відношення несумісності, що відтворене діаграмою Ейлера для висновку під діаграмою засновків.

3. Порівнюємо діаграму висновку з діаграмою засновків і бачимо, що у висновках зафіксоване лише одне з можливих відношень, які зафіксовано в засновках, отже, відношення несумісності не є необхідним, оскільки може бути одне з двох інших відношень. Націй підставі з'ясовуємо, що висновок не є обґрунтованим, отже, вивід - неправильний.

Інструменти. Алгоритм виявлення правильності силогізму методом Джона Венна

1. За допомогою графічних позначень різних видів тверджень, зображених у табл. 6.2, графічно фіксують засновки на діаграмі засновків.

2. Графічно фіксують висновок на діаграмі висновку.

3. Порівнюють діаграму висновку з діаграмою засновків. Якщо на діаграмі висновку позначено як неіснуючі (заштрихованими полями) чи як існуючі (поля, позначені хрестиком) ті об'єкти, які не позначено такими на діаграмі засновків, то роблять висновок - вивід неправильний.

Таблиця 6.2. Графічні позначення у методі Джона Венна

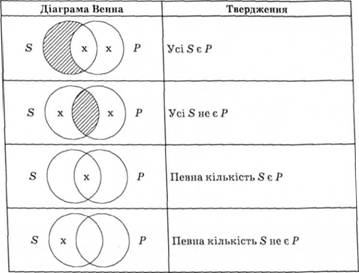
Нижче наведено приклад застосування методу Дж. Венна в разі правильного силогізму.

Проаналізуємо такий силогізм:

Побудуємо діаграму засновків. Насамперед зафіксуємо графічно перший засновок. Згідно з ним, оскільки всі Й є в межах М, то 5 за межами М не існують (тому відповідне поле заштрихуємо - предмети, що відповідають заштрихованому полю, не існують). Водночас предмети з ознакою в існують, і це фіксують хрестиком на полі, яким позначено предмети з ознакою в (це та частина Я, яка збігається з М). Оскільки це поле М розділене на дві частини (ті, які мають ознаку Р, і ті, які її не мають), то хрестик ставимо на межі. Це означає, що чинний один із трьох варіантів (рис. 6.3):

1) існують тільки ті 5, які не є Р;

2) існують тільки ті 5, які є Р;

3) існують і ті, й інші.

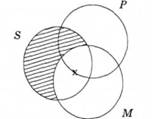
Рис. 6.3

Для повного відтворення відношень, зафіксованих засновками, побудовану діаграму Венна для першого засновку треба доповнити графічним зображенням відношень другого засновку. Подібно до попереднього засновку, оскільки всі М є в межах Р, то М за межами Р не існує (тому відповідне поле заштрихуємо). Унаслідок цього з двох видів предметів 5 (які мають ознаку Р і які її не мають) залишився тільки один - ті в, які мають ознаку Р. Тому хрестик, яким позначили існування предметів б, треба з межі між полями перемістити в середину центрального поля. Крім того, треба позначити, що предмети з ознакою М існують (тобто відповідна підмножина не порожня). Водночас предмети з ознакою М існують, і це фіксують хрестиком на полі, яким позначено предмети з ознакою Р (це та частина М, яка збігається з Р). Оскільки поле Р розділене на дві частини (ті, які мають ознаку 5, і ті, які її не мають), то хрестик ставимо на межі. У підсумку отримали діаграму Венна для засновків (рис. 6.4):

Рис. 6.4

Наступним кроком є побудова діаграми Венна для висновку. Відношення висновку фіксують за тією самою схемою, що й відношення в засновках (рис. 6.5):

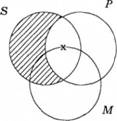
Рис. 6.5

Оскільки висновком зафіксовано, що предмети 5, які мають ознаку Р, існують (відповідна підмножина не є порожньою), і те саме зафіксовано на діаграмі засновків, то силогістичний вивід оцінюють як правильний.

Для виявлення правильності силогізмів можна використати й інші способи графічного позначення відношення між обсягами імен (класами).