Маркетингова цінова політика - Окландер М.А. - 5.1. Метод найменших квадратів і оцінка кривої попиту

5.1. Метод найменших квадратів і оцінка кривої попиту

Цінова політика значною мірою залежить від попиту, який формується як сума індивідуальних попитів. В свою чергу, індивідуальні обсяги попиту залежать від доходів, уподобань покупців та рівня цін. Отже, ринковий попит - це сума індивідуальних попитів, що відповідають певному рівню цін. На попит впливають дві групи чинників:

1) цінові - ціна товару;

2) нецінові - зміна уподобань покупця; зміна цін на субститути і комплементи; кількість покупців; коливання доходів покупців; цінові очікування покупців.

Крива попиту - це графік, який ілюструє залежність між ціною та загальним обсягом попиту всіх покупців.

Між попитом та ціною можливі наступні функціональні залежності:

o лінійна;

o параболічна (квадратична);

o обернена (гіперболічна).

Лінійна залежність. Крива, яка ілюструє лінійну залежність попиту від ціни представлена на рис. 5.1.

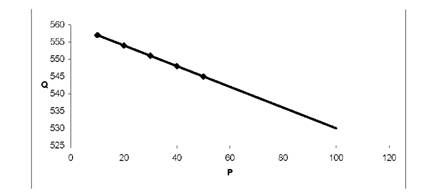
Рис.5.1. Лінійна залежність між попитом та ціною

Параметри лінійної моделі (а0 > 0), (а1 < 0) вказують на те, що при збільшенні ціни попит зменшується рівномірно зі швидкістю (а1). Наприклад, при збільшенні ціни від 20 до 40 одиниць попит зменшиться так само, як і при збільшенні ціни від 60 до 80 одиниць.

Параболічна (квадратична) залежність. Крива, яка ілюструє параболічну (квадратичну) залежність попиту від ціни представлена на рис. 5.2.

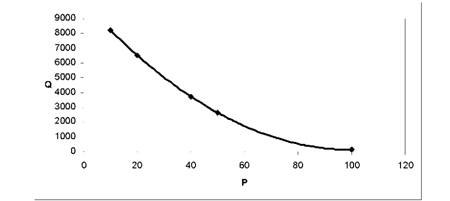
Рис. 5.2. Параболічна залежність між попитом та ціною

Видно, що параболічна крива має параметри моделі (а1 < 0), (а2 > 0) , тобто, має вигляд лише однієї гілки параболи - спадаючої. Якщо (а2 < 0), то крива буде випуклою вверх. На відміну від лінійної моделі, зменшення попиту при збільшенні ціни відбувається прискорено - зі швидкістю (а1 + 2а2р), тобто при збільшенні ціни швидкість падіння попиту зменшується. З рис.5.2 видно, що при збільшенні ціни з 20 до 40 одиниць попит скорочується більше, ніж при збільшенні ціни від 60 до 80 одиниць.

Обернена (гіперболічна) залежність. Крива, яка ілюструє обернену (гіперболічну) залежність попиту від ціни представлена на рис. 5.3.

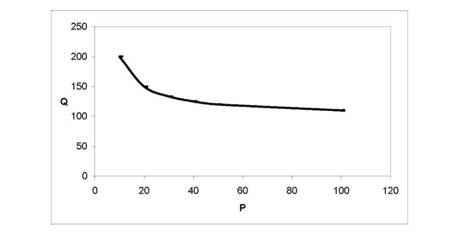
Рис. 5.3. Обернена залежність між попитом та ціною

Математичний вигляд кривої попиту з оберненою (гіперболічною) залежністю описується наступною формулою:

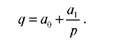
До здійснення продажів ще невідоме математичне рівняння залежності попиту від ціни. На цьому етапі формування ціни відбувається на основі раніше розглянутих чинників ціноутворення. Для пошуку оптимального співвідношення ціни і попиту використовують метод найменших квадратів.

Метод найменших квадратів застосовують, коли емпірична залежність між попитом та ціною відома, наприклад - лінійна, але треба оцінити її параметри. Він використовується для розрахунку параметрів моделі попиту від ціни та вибору найбільш точної, надійної та адекватної моделі (рис. 5.5).

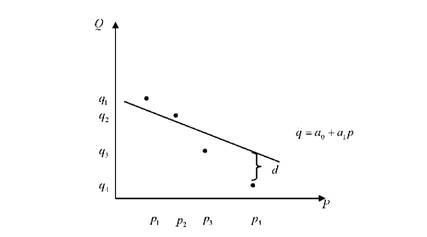
Рис. 5.5. Графічне пояснення методу найменших квадратів

Припустимо, що за результатами спостережень, отримано чотири значення ціни на товар (р1, р2, р3, р4) та значення відповідного попиту (q1, q2,q3, q4). Спершу будемо вважати, що крива попиту від ціни має лінійний вигляд. Тоді, постає питання: Які параметри лінійної моделі слід взяти, щоб пряма проходила якнайближче до точок на площині.

Метод, який дозволяє отримати параметри прямої (або іншої лінії) так, що вона буде проходити якнайближче до точок, зображених на рис.5.5, називається методом найменших квадратів.

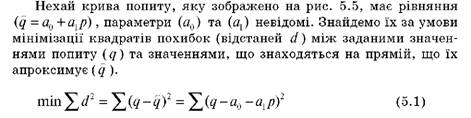
Відомо, що функція набуває найменшого чи найбільшого значення в точках, де її похідна, чи часткові похідні, дорівнює нулю або не існує. Параметри лінійної моделі знаходимо з умови, що частинні похідні функції (5.1) за змінними (а0) та (а1) дорівнюють нулю. Отримаємо формули, за якими знаходять значення параметрів (а0) та (а1) методом найменших квадратів:

Приклад 1. Для дослідження функції попиту від ціни продавець провів пробний продаж нового виду шампуню. Товар пропонувався за різними цінами в п'яти рітейлерських мережах: "Сільпо", "Копейка", "Таврія-В", "Віртус", "Фуршет" (5.1).

Таблиця 5.1. Обсяги продажу шампуню

Перш ніж розраховувати параметри лінійної моделі, побудуємо діаграму розподілу обсягів продажу та цін (рис. 5.6).

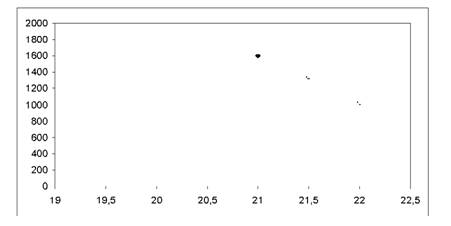
Рис. 5.6. Діаграма розподілу обсягів продажу та цін

Видно, що точки розташовані не на прямій, але й не розкидані далеко від прямої. По-перше, припустимо, що функція попиту лінійна. Щоб розрахувати параметри лінійної моделі за формулами 5.2 та 5.3 побудуємо табл. 5.2.

Таблиця 5.2. Допоміжні дані для отримання параметрів лінійної моделі

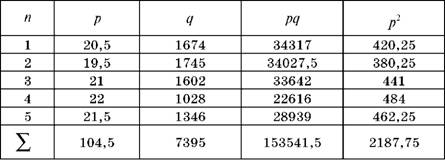
Лінійна функція попиту в розглянутому прикладі має наступний вигляд:

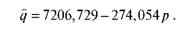
Для знаходження параметрів функції попиту від ціни зручно використовувати табличний процесор EXCEL (рис. 5.7).

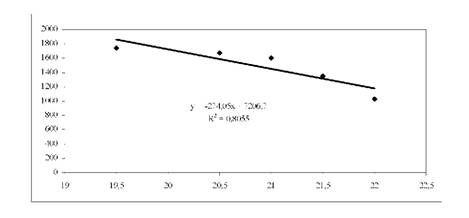
Рис. 5.7. Лінійна функція попиту, отримана в EXCEL

Для цього треба побудувати діаграму розподілу і на графіку за допомогою правої клавіші викликати контекстне меню, де вибрати "Добавить линию тренда". На графіку також можна вивести рівняння моделі та коефіцієнт детермінації (R2), який показує відсоток варіації даних, що пояснюється моделлю. Лінійна функція пояснює 81% варіації даних, оскільки (R2 = 0,8055).

По-друге, припустимо, що функція попиту є параболічною (квадратичною). Скористаємося табличним процесором EXCEL для оцінки параметрів параболічної функції попиту від ціни. Для цього обираємо тип лінії тренду - "поліноміальна другого ступеню". На графік виводимо рівняння кривої попиту та значення коефіцієнту детермінації (рис. 5.8).

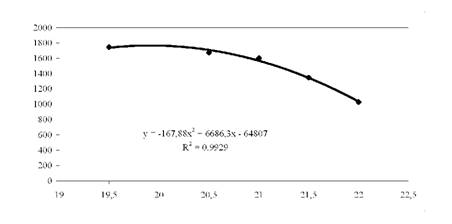
Рис. 5.8. Параболічна функція попиту, отримана в EXCEL

Лінія, що була отримана для апроксимації параболою, знаходиться до точок ближче, ніж пряма. Її рівняння має вигляд:

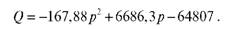
Коефіцієнт детермінації у параболи 99,29%.

По-трєтє, припустимо, що функція попиту є оберненою (гіперболічною). Щоб отримати гіперболічне рівняння кривої попиту від ціни, необхідно побудувати допоміжний стовпчик з даними (табл.5.3).

Таблиця 5.3. Допоміжні дані для отримання гіперболічної (оберненої) кривої

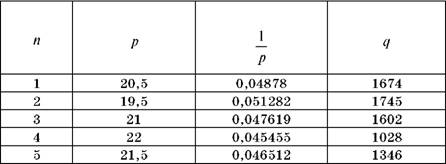
Це рівняння пояснює лише 77,54% варіації даних, що гірше ніж у параболічної та лінійної кривої попиту (рис.5.9).

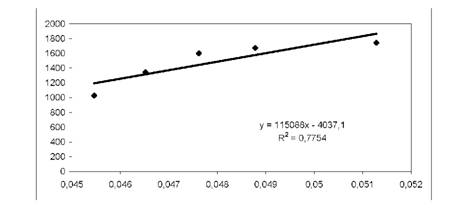
Рис. 5.9. Гіперболічна функція попиту, отримана в EXCEL

Таким чином, для прийняття рішень щодо ціноутворення, оцінки еластичності попиту за ціною та прогнозування попиту краще використовувати параболічну модель попиту, ніж лінійну та гіперболічну.