Статистика - Опря А.Т. - § 2.3. Математичні основи теорії факторного аналізу . Матриця даних

Математичним аспектам сучасного факторного аналізу присвячено ряд робіт (монографій) вітчизняних і зарубіжних авторів. Як вид багатомірного статистичного аналізу, він, має свої сильні і слабкі сторони. Щоб мати уяву про це, необхідно поставити завдання дослідження теоретичних аспектів факторного аналізу, як науки.

В даному параграфі будуть розглянуті лише деякі основні елементи даного статистико - математичного методу в той мірі, в якій це необхідно для розуміння його практичної реалізації в економічних розрахунках.

Перш за все тут потрібний деякий обсяг елементарних математичних знань з алгебри, аналітичної геометрії і тригонометрії, а також розділів математики, у яких висвітлюються питання матричної алгебри.

Економіко - математичні моделі, що використовуються сьогодні в різного роду економічних розрахунків, часто призначені для опису взаємозв'язку економічних структур, їх зміни в часі і просторі, залежності від ряду факторів і т.д. Вважається, що одним з найкомпактніших способів опису таких структур (інколи дуже складених) є спосіб матричного відображення.

Фактор, як розрахункова змінна у факторному аналізу, являє собою деяку нову характеристику об'єктів досліджуваної множини. Розгляд (опис) його через призму набору вихідних ознак досягається шляхом розрахунку так званої матриці. У факторному аналізі загальновживаний термін "матриця факторів" або "факторна матриця". Інколи її називають "матрицею факторних навантажень"

Інакше, матриця - це прямокутний масив чисел, розташованих за рядками і стовпчиками. Така форма подання числових даних є зручною для їх математичної обробки. Перевага матричної форми запису полягає в тому, що в невеликому наборі символів не мов спресована множина математичних операцій, що надзвичайно зручно при аналізі масових даних. Перш за все перевага виявляється на початковому етапі обробки інформаційного масиву, тобто на етапі організації вихідних даних. Наприклад, розглянемо дані про середньорічні надої залежно від рівня годівлі корів і року їх лактації (табл. 108 ).

Таблиця 108

Середньорічний надій корів в залежності від лактації і рівня годівлі, кг

Наведену табличну інформацію можна записати у такій формі:

3500 3700 3900

3600 3900 4300

4100 4300 4700

4500 5000 5500

Змістовне значення кожного показника визначається його місцем в даному масиві. Так, число 4300 в третьому рядку і другому стовпчику являє собою надій корів на третьому році лактації при рівні годівлі 40-45 ц кормових одиниць в рік. Аналогічно визначаємо, що числа, які занесені у стовпчик, характеризують надій при однаковому рівні годівлі, але в різні лактаційні періоди, а числа, які записані в рядок, - надій корів одного і того ж року лактації, але при різному рівні годівлі. Отже місце, що займає число в масиві, характеризує період лактації і рівень годівлі, до якого відноситься надій.

Як бачимо, елементи рядка чи кожного стовпчика володіють якоюсь загальною властивістю. Елементами матриці. можуть бути числа будь - якого виду чи навіть функцій однієї чи кількох змінних. Над числовими масивами такого типу можуть бути виконані різні алгебраїчні операції. При цьому виходять з припущення, що кожний масив є єдине ціле і позначається одним символом. У подальших міркуваннях будемо виходить з того, що елементи матриці є дійсні числа - додатні, від'ємні або нуль.

Доречно буде нагадати, що під матрицю розуміють прямокутну або квадратну таблицю чисел, яку розглядають безвідносно до існуючих (чи неіснуючих) зв'язків між ними. Тобто є числа, розташовані у вигляді рядків і стовпчиків, мають формальну математичну схему, байдужну до природи заздалегідь визначених залежностей між цими числами.

Якщо позначити матрицю факторних навантажень через А, число ознак через п, число факторів - через т, то порядок або розмірність матриці складе п х т. Квадратна матриця, (п х п) має розмірність п.

Елементи матриці позначаються двома підрядковими індексами, перший з яких означає номер рядка, другий - номер стовпчика. Наприклад, символ х₃₂ вказує на елемент, що знаходиться на перетині третього рядку і другого стовпчика .

Хц Хц

х31 х32 х33

Схема квадратної матриці розмірністю 3 х 3 У загальному вигляді матриця записується такому вигляді

Хц ^х13^... Хг_п

Хц ^Х22 ^Х ₂₃........

...... ^Хч ^... '

Схема загального виду матриці

Загальний елемент матриці ^означає, що індекс рядка |і| може приймати послідовне значення 1,2,3,...,т, а індекс стовпчика |у|-

послідовне значення 1,2,3, ... п. Матриця А може бути виражена через загальний її елемент X,-,-.

Якщо рядки матриці стають стовпчиками, ми одержуємо нову матрицю, яка буде транспонована по відношенню до матриці А. На схемі наведена матриця А і її транспонування (матриця А').

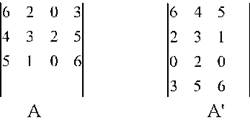
Схема транспонування матриці А

Мають місце випадки, у факторному аналізі, коли квадратна матриця збігається з транспонованою до неї матрицею, тоді матрицю А називають симетричною.

6 2 1

2 6 4 = А = А'. 1 4 8

Схема симетричної матриці.

У факторному аналізі має місце, як правило, робота з симетричними матрицями. Прикладом такого виду може бути матриця, елементи якої представлені коефіцієнтами кореляції змінних сукупності, що вивчається.

Алгебраїчні операції над числовими масивами, поданими у вигляді матриць, вивчає матрична алгебра, предметом якої є дії не з окремими елементами, а безпосередньо з масивами. Останні виступають як відокремлені і цілісні системи.

Основні арифметичні дії з матрицями - це додавання, віднімання і множення.

Розглянемо порядок здійснення названих арифметичних операцій.

Додавання матриць. Наприклад, є дані про виробництво продукції підприємством за липень (табл.109).

Таблиця 109

Обсяг виробництва продукції підприємством за липень, т

Зміст таблиці в матричній формі з розмірністю 3 х 3, буде таким:

66 72 24

А = 42 63 60 . 30 50 40

Маючи аналогічні дані про обсяг виробництва продукції в наступному місяці (серпень), запишемо їх у такому ж порядку у вигляді матриці:

34 42 30

В = 30 50 25.

26 40 42

Загальний обсяг виробництва по виду продукції 0₄, виробленої в першій бригаді, дорівнює сумі елементів, розташованих в кожній матриці на перетині першого рядка і першого стовпчика: 66+34=100, а загальний обсяг виробництва продукції 0₂ за два місяці по третій бригаді становить 60+25=85. Матриця в такому випадку матиме вигляд :

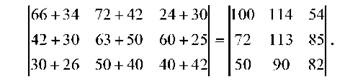
Числа, одержані в результаті додавання елементів двох матриць, характеризують (у даному випадку) обсяг виробництва різних видів продукції по бригадах за два місяці. Таким чином, сума двох матриць являє собою матрицю, кожний елемент якої є сума відповідних елементів матриць - доданків.

Додавання матриць можливо лише у випадку однакової їх розмірності (тхи), тобто однаковій кількості рядків (т) і однаковій кількості стовпчиків (п). Такі матриці називають узгодженими для додавання.

Додавання матриць 3 2 4 * ^{26 не має зм}і^стУ

Якщо прийняти позначення А = {я_у.} і в = }, то сумою матриць А і В буде матриця А + в = ^ + в_ц}.

Віднімання матриць. Подамо дані про виробництво продукції за серпень за розглянутим вище прикладом з додаванням матриць у вигляді таблиці 110.

Таблиця 110

Обсяг виробництва продукції підприємством за серпень, т

У матричному відображенні зміст таблиці матиме вигляд:

34 42 30

В = 30 50 25 .

26 40 42

Подамо обсяг виробленої продукції підприємством за липень також у вигляді матриці:

66 72 24 А = 42 63 60 . 30 50 40

Щоб визначити зміну в обсязі виробництва продукції 0₁ в серпні порівняно з липнем, наприклад, в бригаді 3, необхідно від 30 відняти 24; по продукції 0₂ відповідно 25-60 і т.д.

Подамо різницю в обсязі виробництва за два місяці в розрізі бригад і видів продукції в матричному відображенні:

34 - 66 42 - 72 30 - 24 - 32 - 30 6 30- 42 50 - 63 25 - 60 = -12 -13 -35 . 26 - 30 40 - 50 42 - 40 - 4 -10 2

Одержана матриця характеризує різницю в обсягах виробництва продукції різних видів у серпні порівняно з липнем по всіх бригадах. Проведені розрахунки ілюструють приклад віднімання матриць. Схематично це виглядає на умовному прикладі так:

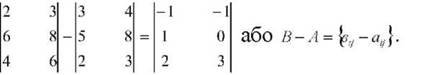
Здійснювати операцію віднімання можна тільки із матрицями, що мають однакову розмірність (порядок). Інакше кажучи, матриці узгоджені для додавання, узгоджені і для віднімання (і навпаки).

Множення матриць. Правило множення матриць випливає з правила їх додавання. Якщо подати : А + А = ^+^>(і_ІІ}={2х_ц}= 2А, то для випадку, коли Б - ціле додатне число, можна записати у вигляді БЛ= Л+Л+Л+...+А.

Згідно з правилом додавання матриць одержимо:

Для скалярних величин (в даному випадку Б) і матриць добуток виглядатиме як матриця, в якій кожний елемент помножено на Б.

Наприклад, при Б= 6 і матриці ^ ⁶ добуток матиме вигляд:

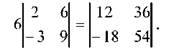
При множенні матриці на матрицю необхідно уявити многократне множення матриці на вектори. Так, при множенні матриці А на матрицю В подаємо матрицю В як набір векторів -стовпчиків. В такому випадку добуток АВ виглядатиме як послідовно записані один за одним добутки матриці А на кожний вектор - стовпчик, що утворює В.

Приклад. Маємо дві матриці:

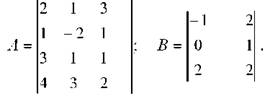
Матрицю В подамо у вигляді двох векторів - стовпчиків:

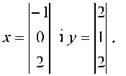
Помноживши матрицю А на кожний з векторів - стовпчик матриці В, маємо;

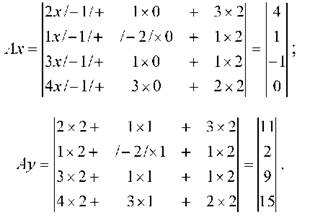
Розмістивши вектори один за одним, маємо добуток матриці АВ:

Проведені операції в повному їх вигляді мають вид :

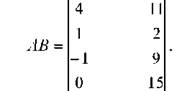
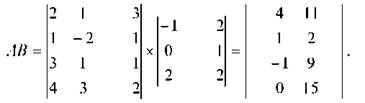
До одержаного результату можна дійти іншим шляхом, послідовно перемноживши елементи матриць А і В, рухаючись по горизонталі впродовж і - того рядка матриці А і одночасно - вниз по ) - тому стовпчику матриці В, потім додавши між собою всі ці добутки.

Сума добутків відповідних елементів утворює у - й елемент матриці -добутку АВ.

Діючи за такою схемою, послідовно множимо елементи третього рядка матриці А на елементи першого стовпчика матриці В:

3 х (-1) + 1х 0 + 1х 2 = -3 + 0 + 2 = -1.

Таким чином, елемент, що стоїть в третьому рядку матриці А і першому стовпчику матриці В, дорівнює -1.

Добуток матриць Аі В має зміст лише у тому випадку, коли і - й стовпчик матриці В (отже, і всі інші стовпчики) налічує таку ж кількість елементів, що й і-й рядок матриці А (отже, і всі інші її рядки).

Таким чином, в матриці В повинно бути стільки ж рядків, скільки стовпчиків має матриця А. Отже, добуток матриць А і В визначено тільки у випадку, коли число стовпчиків в матриці А дорівнює числу рядків в матриці В. Такі матриці називають узгодженими для множення А на В.

Приклад. Маємо матриці:

1 2 5

0 3

А= ; В= 4 3 8.

6 2 '

Оскільки А містить два стовпчики, а В- два рядки, існує добуток АВ.

1 2 5 12 9 24

0 3

АВ = х 4 3 8 =14 18 27 .

62

Розмірність (порядок) добутку АВ складає 2 х 3. У даному випадку добуток ВА не існує, бо матриця В містить три стовпчики, а матриця А - два рядки.

Згідно з законом матричної алгебри перед виконанням операцій додавання, віднімання і множення необхідно з'ясувати питання про узгодженість матриць.

Крім розглянутих вище з матрицями, існують й інші. Це-множення векторів, множення на діагональну матрицю, лінійні перетворення, трансформування матриць і т.д. Названі операції докладно викладені в курсі матричної алгебри.

У факторному аналізі найчастіше зустрічаються такі види матриць: діагональна, скалярна, одинична, обернена.

Діагональна матриця - квадратична матриця, яка відрізняється від нуля тільки елементами, що лежать на діагоналі, яка зв'язує верхній лівий край з правим нижнім краєм матриці (головна діагональ).

Скалярна матриця - діагональна матриця, в якій всі елементи рівні між собою.

Одинична матриця - діагональна матриця, в якій всі елементи головної діагоналі дорівнюють одиниці. Цей вид матриці виконує в матричній алгебрі ту ж роль, що й одиниця в арифметиці.

Обернена матриця . Подавши найпростішу арифметичну

залежність у вигляді х ■- = і, яка означає, що добуток будь - якого

х

числа на обернене йому число дорівнює одиниці, можна знайти аналогічний зв'язок і в матричній алгебрі. Якщо матриця А квадратна, то існує матриця, обернена їй А^-1, або А■ А'¹ = і.

Спосіб обчислення оберненої матриці досить складний. Названі види матриць схематично представлено:

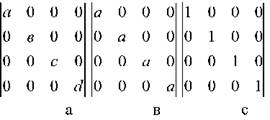
Схеми видів матриць, які зустрічаються у факторному аналізі (а- діагональна, в - скалярна, с- одинична)