Статистика - Опря А.Т. - § 2.5. Виділення факторів і визначення їх навантажень

Вихідним початком факторного аналізу є складання кореляційної матриці, а його метою - побудова факторної матриці. Отже, розв'язується завдання виділення факторів. Серед існуючих способів розв'язання цього завдання найпростішім і загальним методом виділення факторів є так званий центроїдний метод. При розгляді конкретного прикладу виділення факторів і визначення їх навантажень будемо користуватися названим вище методом без викладання його теоретичних аспектів. Останні розглядаються в спеціальній математичній літературі.

На початковому етапі виділення факторів складається матриця коефіцієнтів кореляції. Організувавши редуковану кореляційну матрицю, переходять до редукованої факторної матриці. Остання повинна показувати кількість загальних факторів, відображуючи кореляцію між змінними, які вивчаються. Тут число загальних факторів відповідає числу стовпчиків редукованої факторної матриці. По цій же матриці маємо навантаження кожного фактору для тієї чи іншої змінної. Це - рядки факторної матриці.

Згідно з існуючою теоремою, редукована матриця кореляції дорівнює добутку редукованої факторної матриці на транспоновану. Схематично це має такий вигляд:

З наведеної залежності (Я=РР') випливає рівняння, яке має важливе практичне значення, що дозволяє встановити кореляцію на підставі факторних навантажень. Наприклад, якщо маємо п некорольованих факторів С, загальних для змінних а і в, то кореляція межі а і в (г_ав) дорівнює сумі добутків навантажень кожного з факторів на ці змінні:

^Гае = ^Га^СГе С + ^Га^С1 ^Ге^С2 + - + ^Га^Сп ^Ге^Сп Д^Є

^га^сг_в^с - навантаження фактора С₁ при змінних а і в; г_ас₂т_вс₂ - навантаження фактора С₂ при змінних а і в;

к с_п - навантаження п - го фактора, загального для обох

змінних.

Наведене вище рівняння дозволяє визначити кореляцію між двома змінними, якщо відомі навантаження загальних для цих змінних факторів. У практичних розрахунках завжди вирішується протилежне завдання: визначити факторні навантаження на підставі існуючих кореляцій.

Якщо припустити існування загального фактора С₁ при відомих кореляціях змінної а з трьома іншими змінними е,с,й , то кожна з змінних буде характеризуватися навантаженням загального фактора такими рівняннями: r_ao = (r_aC₁) x (r₀Q); r_ad = (T.C,) x (r^).

Як бачимо, у правій часті наведених рівнянь існує однаковий параметр r_aC_l . у цьому зв'язку існуюча теорема свідчить, що середня кореляція змінної з іншими змінними, розрахованаі з суми всіх кореляцій (у стовпчику), пропорційна кореляції цієї змінної з загальним фактором r_aC_x.

у практичних розрахунках середня кореляція розраховується шляхом ділення суми елементів одного стовпчика на корінь квадратний з суми всіх стовпчиків матриці. у цьому і полягає суть виділення факторів за матрицею парних кореляційних залежностей.

Приклад. У кореляційно-регресійну модель урожайності зернових культур (у) включено шість факторів затрати праці на 1 га зернових (xf); вартість основних виробничих фондів в розрахунку на 1 гектар ріллі (х₂); матеріально - грошові затрати виробництва з розрахунку на 1 гектар зернових (х₃); виробництво зерна на 1 людино - годину (х₄); вартість основних виробничих фондів з розрахунку на одного працівника рослинництва (х₅); оплата 1 людино - години в зерновому господарстві (х₆) .

Як бачимо, поставлене аналітичне завдання: одержати кількісну характеристику змін урожайності під впливом факторів інтенсифікації виробництва (х;,х₃), фондооснащеності (х₂) і фондоозброєності (Xj), продуктивності праці (х₄) та її оплати (х₆). У вибірку включено 57 одиниць спостереження.

У результаті обробки вихідної інформації на ПЕОМ одержано кореляційна матриця: (табл. 111).

Таблиця 111

Матриця вихідних коефіцієнтів кореляції

Величина одержаного множинного коефіцієнта кореляції (Я) по досліджуваній моделі становить 0,761. Початку пошуку загального для всіх змінних фактора передує побудова редукованої кореляційної матриці (табл.111).

По головній діагоналі цієї матриці заносяться величини максимальних значень коефіцієнтів кореляції у стовпчику (без врахування алгебраїчних знаків). На наступному етапі розраховують навантаження першого загального фактора. З цією метою виконують такі обчислювальні операції:

а) відшукують суми параметрів по стовпчиках з врахуванням алгебраїчних знаків;

б) визначають суми сум стовпчиків. У нашому випадку ця величина (Т) становить 2,623. Потім обчислюють її корінь квадратний: чІТ = 1,61957;

в) одержані по стовпчиках суми ділять на 4~Т, маючи, таким чином, навантаження першого фактора для шести змінних, тобто - їх кореляцію з досліджуваним фактором. У символіці навантаження першого фактора С₁ для змінної а має такий вигляд:

V г

^Си ~ чіт o

Ця характеристика записана в останньому рядку таблиці 111;

г) як критерій правильності розрахунків використовують додатково

обчислену величину -^=. У нашому прикладі її значення дорівнює 0,61745. Як

ч/Т

бачимо, при умові правильності розрахунків Т = 4т . У прикладі :

чІТ

2,623 х 0,61745 = 1,61957 , що повністю збігається з розрахованою величиною чІТ .

Другим критерієм правильності розрахунків є сума всіх факторних навантажень . її величина повинна також дорівнювати 4~Т. У наших розрахунках £С₁ = 1,620 при чІТ =1,61957. Розрахунком розглянутих критеріїв завершується аналіз редукованої кореляційної матриці з метою визначення навантажень першого, загального для всіх змінних фактора (табл.112 ).

Таблиця 112

Т=2,623; чІТ = 1,61957; = 0,61745.

' ' ' ' ЧІТ

Критерій Т --^ = 1,61957. Критерій = 1,620.

Для виділення навантажень решти факторів виходять з теоретичної концепції (існує теорема) про те, що кореляція двох змінних, викликана яким -небудь загальним для них фактором, дорівнює добутку навантажень цього фактора для обох змінних, тобто добутку їх кореляцій с цим фактором. Так, кореляція між першою і другою змінними Р₄ і Р₂, зумовлена першим фактором, являє собою добуток його навантажень по першій і другій змінних. Виходячи з наведених вище розрахунків, маємо:

^гр,р_г ^{= г}_-с₂ ^{х г}р₂с, = 0-119 х 0.404 = 0.048.

Одержаний за розрахунками коефіцієнт кореляції між змінними Р₄ і Р₂ дорівнює 0,175. Щоб визначити частину дисперсії, яка може бути зумовлена іншими факторами, знаходять так званий "залишок " шляхом віднімання з початкового коефіцієнта кореляції між змінними (г_рір5 = 0,175) величини коефіцієнта кореляції, зумовленої першим фактором (г= 0,048) Тоді маємо

0,175-0,048=0,127.

У випадку одержання від'ємного залишку слід пам'ятати, що навантаження досліджуваного фактора у відповідних змінних мають від'ємний знак.

За даними нашого прикладу, для кожної пари змінних знаходимо: різницю між значенням початкових коефіцієнтів кореляції і добутком факторних навантажень:

г = 0.659 - 0.119 х 0.119 = 0.645;

Рі Рі ³

г = 0.175 - 0.119 х 0.404 = 0.127;

г = 0.136 - 0.119 х 0.293 = 0.101; г = (-0.659) - 0.119 х 0.036 = -0.663; г = 0.073 - 0.119 х 0.344 = 0,032; г = (-0.191) - 0.119 х 0.424 = -0.241.

Подібні розрахунки зручніше здійснювати у вигляді робочих таблиць. При цьому слід враховувати алгебраїчні знаки (табл. 113 і 114).

Таблиця 113

Матриця добутків факторних навантажень

Матриця перших залишків кореляцій

Таблиця 114

Для розрахунку навантажень другого фактора необхідно визначити середню кореляцію кожної змінної з іншими змінними.

З цією метою розраховують суми по стовпчиках матриці перших залишків (табл.114). Слід знати, що мірилом правильності розрахунків є критична величина "0,010". Суми по стовпчиках не повинні перевищувати її рівень. У нашому прикладі розрахунки, як бачимо, вірні.

Оскільки додатні і від'ємні значення коефіцієнтів кореляції урівноважуються, сума всіх стовпчиків матриць практично буде дорівнювати нулю. Розрахунок навантажень другого фактора можна здійснювати лише при наявності додатніх сум елементів стовпчиків матриці. З цією метою необхідно виконати перетворення алгебраїчних знаків у матриці залишків кореляцій. (Ця математична процедура не змінює абсолютне значення коефіцієнта кореляції. З точки зору графічної інтерпретації конфігурація векторів змінних зберігає свій зміст, оскільки змінюється лише напрямок змін змінних).

Розрахунок навантажень другого фактору здійснюється у такій послідовності:

1. Визначають алгебраїчну суму елементів по стовпчиках, виключаючи елементи головної діагоналі ( у табл.64 рядок У^г₀). Знайдені суми додають по рядку (ііг₀). У розглядуваному прикладі ця величина дорівнює - 1,836.

2. Відшукують стовпчик з найбільшою від'ємною сумою (стовпчик Р^ - 0,668).

Ця сума з додатним знаком записується в рядок з назвою "Стовпчик 4" по вертикалі даного стовпчика.

Подальші розрахунки по рядку здійснюють у такій послідовності: до суми стовпчика додають з протилежним знаком подвоєне значення елемента цього стовпчика, який знаходиться на перетині з "перетворюваним рядком". Одержаний результат записують у рядок, з назвою "Стовпчик 4". У нашому випадку, наприклад, величину 0,682 одержуємо: -0,644 -2 х 0,663; величину 0,165 маємо при розрахунку: - 0,093 -2 х 0,129 і т.д. Обчислені елементи (суми) даного рядка підсумовуємо і заносимо у графу 8

( 1,262).

Таблиця 115

Розрахунки навантаження другого фактора (перетворення знаків у матриці перших залишків кореляції)

Далі відшукуємо наступний стовпчик з найбільшою від'ємною сумою. Послідовність розрахунку нового рядка аналогічна описаній вище. Одержанні елементи рядків додаємо на стовпцях, одержуючи значення xг - Подальші обчислення виконують у послідовності, аналогічній описуванню розрахунків по визначенню навантажень першого фактора. Навантаження другого фактора для змінної а визначають за уже відомою формулою:

С_1а - навантаження другого фактору для змінної а;

^ г_а - сума по стовпчику а;

Т - загальна сума всіх коефіцієнтів матриці.

При обчисленні факторних навантажень виникають певні математичні тонкощі, зв'язані з перетворенням знаків матриці, розрахунком певних критеріїв, а також деякими методичними особливостями виділення факторів. Викладення математичних основ цієї сторони обчислювальних дій виходить за рамки нашої роботи. Тут необхідно звертатися до спеціальної літератури.

Логічним завершенням здійснюваних розрахунків у справі вичленування факторів слід назвати етап припинення виділення факторів. Серед множин існуючих методик Я. Окунь посилається на метод під назвою "Критерій Саундерса" .

Суть і послідовність обчислювальних операцій за вказаним методом така :

1. Залишки, отримані після виділення К-го фактора, підносять до квадрата і сумують, виключивши елементи головної діагоналі і позначивши число змінних п. Одержана сума множиться на -^2п- з

п -1

метою приведення її у відповідність з повною матрицею. Одержана величина становить значення А.

2. Різниця між кількістю змінних і уже виділених факторів ділитися на число змінних. Результат підносять до квадрату. Одержують величину значення В.

3. Факторні навантаження підносять до квадрата, включивши навантаження К-го фактора, і сумують одержані величини. Число факторних навантажень тут дорівнює К х п. Результат віднімають від числа змінних (п) і одержане значення підносять до квадрата. Результат ділять на кількість одиниць спостереження. Одержують значення С.

4. У випадку А < в х с виявлення факторів припиняють. При А у В х с вичленовують наступний фактор і здійснюється описана процедура перевірки.

Приклад. Розглянемо викладену вище методику послідовних операцій на прикладі матриці перших залишків кореляції (табл. 116.). Піднісши до квадрата перші залишки кореляцій, знаходимо їх суму, яка дорівнює 1,583939. Далі знаходимо похідні:

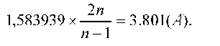
Таблиця 116

Вихідні і розрахункові дані матриці перших залишків

Різниця між числом змінних і числом уже виділених факторів становить 6-1=5 (В).

Подальші обчислювальні операції, викладені вище в пункті 3, зводяться до знаходження значення С. Обчислена сума квадратів факторних навантажень становитиме 0,562634 (^С-0). її різниця з числом змінних дорівнює 6-

0,563=5,437. Квадрат даної величини приймає значення 29,561. Знаходимо

значення С: 29,561: 57=0,519 (С). Добуток В х С дорівнює 2,595. Як випливає з

проведенних розрахунків А у В х С (3,801 >-2,595).Отже за даною кореляційною

моделлю врожайності необхідно продовжити дослідження, пов'язане з

вичленуванням наступного фактора.

У тій же монографії Я.Окунь торкається проблеми мінімізації числа

змінних (п) для визначення однозначного числа факторів ( т).

" , " 2т +1 + V 8т +1 іут автор наводить формулу іерстоуна: п =-^--

Після перетворення формули для одержання числа факторів т маємо:

2п +1 -4 8п +1 п =-.

2

Однозначне число факторів, що вичленовуються для нашого випадку

2 х 6 +1 -V 48 +1 "

становитиме: п =-= 3.

2

Як бачимо, в розглядуваній кореляційно - регресійній моделі урожайності з шістьма змінними можна визначити не більше трьох факторів.

Стандартна таблиця співвідношень числа змінних (п ) і факторів, які вичленовуються має значення: