Теорія статистики - Мармоза А.Т. - 9.5. Статистична оцінка вибіркових показників зв'язку

У тих випадках, коли вивчення кореляційної залежності базується на вибіркових даних, виникає потреба оцінки вибіркових показників кореляції (коефіцієнтів регресії і кореляції).

Статистична оцінка вибіркових показників кореляції дає змогу зробити висновок про те, наскільки вибіркові статистичні показники відповідають показникам генеральної сукупності. Однак така оцінка проводиться у випадках, коли: 1) вибірка сформована у випадковому порядку; 2) вибірка зроблена з нормально розподіленої сукупності; 3) відхилення фактичних значень результативної ознаки від її теоретичних значень, обчислених за рівнянням, також розподілені нормально.

Розглянемо порядок статистичної оцінки вибіркових показників зв'язку при парній лінійній регресії.

В кореляційному аналізі середня помилка вибірки обчислюється на основі залишкової дисперсії, оскільки ця величина характеризує точність підбору кривої до фактичних даних. Проте залишкова дисперсія, розрахована за вибірковими даними, зменшує дійсну величину залишкової дисперсії в генеральній сукупності, тобто є зміщеною оцінкою. Це зміщення коригується внесенням в знаменник формули залишкової дисперсії поправки на втрату ступенів свободи. При парній лінійній залежності втрачаються відповідно числу параметрів рівняння (а і Ь) дві ступені свободи, при кореляції трьох змінних з параметрами а, Ь і с - три ступені свободи і т.д.

Квадрат середньої помилки вибіркового коефіцієнта регресії являє собою відношення залишкової дисперсії, скоригованої на втрату числа ступенів свободи варіації, до суми квадратів відхилень незалежної змінної.

Позначаючи залишкову дисперсію через °ух , а квадрат середньої помилки вибіркового коефіцієнта регресії через Мв , одержимо

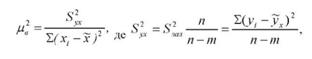
де т - кількість параметрів рівняння регресії, яке дорівнює двом при парній лінійній залежності; п - чисельність вибірки. Відповідно середня помилка коефіцієнта регресії:

Гранична помилка вибіркового коефіцієнта регресії визначається за формулою:

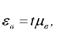
де і - значення нормованого відхилення, величина якого встановлюється за таблицями. Для великих вибірок (п > 30) значення X знаходять за дод. 2, для малих вибірок (п < 30) - за дод. 3.

Довірчі межі коефіцієнта регресії у генеральній сукупності (Ь0) становитимуть:

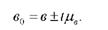
Вірогідність вибіркового коефіцієнта регресії визначається як відношення:

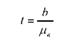
Якщо /факт > гтабл при заданому рівні значущості і відповідному числі ступенів свободи варіації, то нульова гіпотеза про рівність коефіцієнта регресії у генеральній сукупності нулю (Ь0 = 0) відхиляється і робиться висновок про те, що вибірковий коефіцієнт регресії є вірогідним якщо ж /фак! < /табл, то нульова гіпотеза приймається і робиться висновок про те, що значення Ь у вибірці є неістотним, випадковим.

Обчислимо середню і граничну помилку для коефіцієнта регресії, що характеризує залежність продуктивності корів від рівня годівлі (Ь = 0,813 ц).

Визначимо залишкову дисперсію, використовуючи коефіцієнти рівняння регресії У, = 3,22 + 0,813 х і дані табл. 9.1.

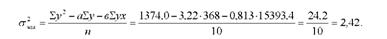
Обчислимо скориговану залишкову дисперсію

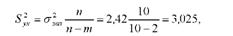
де т - число параметрів рівняння регресії (т = 2).

Визначимо середню помилку параметра Ь: і-:- _

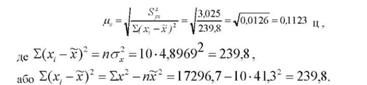
Перевіримо вірогідність вибіркового коефіцієнта регресії Ь, висунувши нульову гіпотезу, а саме: коефіцієнт регресії в генеральній сукупності дорівнює нулю: Н0: Ь0 = 0; На : Ь0 ф 0.

Розрахуємо фактичне значення і - критерію Стьюдента:

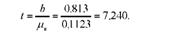
За таблицею (дод. 3) при а = 0,05 і числі ступенів свободи к = п - т = 10 - 2 = 8 знайдемо і0,05 = 2,307.

Оскільки іфакг > і005 (7,240 > 2,307), від нульової гіпотези, яка передбачає відсутність зв'язку між урожайністю і якістю Грунту в генеральній сукупності (Ь0 = 0), слід відмовитись. Вибірковий коефіцієнт регресії Ь = 0,813 є вірогідним, істотним.

Обчислимо граничну помилку вибіркового коефіцієнта регресії:

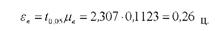
Визначимо інтервал, в якому із заданим рівнем значущості знаходиться коефіцієнт регресії в генеральній сукупності:

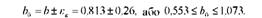
Отже з рівнем значущості а = 0,05 (з імовірністю помилитись в 5 випадках із 100) можна стверджувати, що величина коефіцієнта регресії, який характеризує зв'язок між продуктивністю корів і рівнем годівлі в генеральній сукупності, перебуває в інтервалі від 0,553 до 1,073 ц на 1 ц кормових одиниць.

Для перевірки вірогідності вибіркового коефіцієнта кореляції визначають його середню і граничну помилки вибірки.

Середня помилка вибіркового коефіцієнта кореляції визначається за формулою:

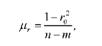
де г0 - значення коефіцієнта кореляції в генеральній сукупності, яке наближено замінюється значенням вибіркового коефіцієнта кореляції; п - чисельність вибірки; т - число параметрів рівняння регресії.

Застосування цієї формули пов'язано з двома обмеженнями: 1) чисельність вибірки повинна бути достатньо великою; 2) вибірковий коефіцієнт кореляції не повинен бути близьким до одиниці. У тих випадках, коли вибірковий коефіцієнт кореляції близький до одиниці (г > 0,8), для перевірки гіпотези про його вірогідність рекомендується застосовувати метод перетвореної кореляції, запропонований Р. Фішером.

Гранична помилка вибіркового коефіцієнта кореляції визначається за формулою:

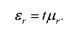
Довірчі межі, в яких знаходиться значення коефіцієнта кореляції в генеральній сукупності, становитимуть

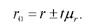
Вірогідність вибіркового коефіцієнта кореляції визначається як відношення

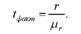
Якщо іфакг > ітабл, то нульова гіпотеза про рівність нулю коефіцієнта кореляції у генеральній сукупності відхиляється і робиться висновок про вірогідність одержаного за вибіркою коефіцієнта кореляції. Якщо ж < ітабл, то нульова гіпотеза приймається і робиться висновок про те, що отримане за вибіркою значення коефіцієнта кореляції неістотне, має випадковий характер.

Крім розглянутого прийому, оцінка вибіркового коефіцієнта кореляції може бути проведена більш простими способами. Для визначення вірогідності вибіркового коефіцієнта кореляції можна користуватися спеціальними таблицями (дод. 9), в яких наводяться критичні значення коефіцієнта кореляції при заданому рівні значущості (а) і відповідному числі ступенів свободи варіації (к = п - т).

Якщо при заданому а і відповідному к фактичне значення вибіркового коефіцієнта кореляції більше табличного значення (гта6л), то тіснота зв'язку між досліджуваними ознаками вважається вірогідною і навпаки.

Проведемо оцінку вірогідності вибіркового коефіцієнта кореляції, що характеризує тісноту зв'язку між продуктивністю корів і рівнем годівлі (г = 0,9344).

Оскільки у прикладі чисельність вибірки невелика (п = 10), а вибірковий коефіцієнт кореляції близький до одиниці (г = 0,9344), оцінку його вірогідності проведемо за допомогою методу Р. Фішера, який дістав назву перетвореної кореляції.

Р. Фішер довів, що розподіл логарифмічної функції вибіркового лінійного коефіцієнта кореляції (2) наближається до кривої нормального розподілу навіть при невеликому обсязі вибірки і високому значенні г.

Величина 2 визначається за формулою

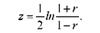
Перехід від г до 2 і назад здійснюється за допомогою спеціальних таблиць, що виключають потребу логарифмування.

Середня квадратична помилка 2-розподілу залежить тільки від обсягу вибірки і визначається за формулою:

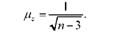
Обчислимо середню помилку 2-розподілу для нашого прикладу

За таблицею (дод. 8) знайдемо, що коефіцієнту кореляції г = 0,9344 відповідає 2 = 1,658.

Визначимо відношення 2 до середньої помилки вибіркового коефіцієнта кореляції:

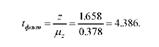
Знайдемо табличне значення і-критерію Стьюдента (дод. 3) при а = 0,05 і к = 10 - 2 = 8; /0,05 = 2,307.

Оскільки фактичне відношення і виявилося більше табличного і005 (4,386 > 2,307), то можна зробити висновок про те, що висунута гіпотеза про рівність нулю коефіцієнта кореляції у генеральній сукупності не узгоджується з фактичними даними в зв'язку з чим вона повинна бути відхилена. Вибірковий коефіцієнт кореляції є вірогідним, істотним.

Побудуємо довірчий інтервал, в якому із заданим рівнем значущості знаходиться коефіцієнт кореляції в генеральній сукупності:

г0 = 2 ± і/4 =1,658 + 2,307 o 0,378 = 1,658 ± 0,872, тобто від 0,786 до 2,530.

Користуючись таблицею значень 2 у зворотному порядку, знайдемо границі довірчого інтервалу для коефіцієнта кореляції в генеральній сукупності:

0,66 < г0 < 0,99.

Отже, із заданим рівнем значущості а = 0,05 можна стверджувати, що тіснота зв'язку між продуктивністю корів і рівнем годівлі в генеральній сукупності знаходиться в межах від 0,66 до 0,99.

Вірогідність вибіркового коефіцієнта кореляції може бути встановлена і без обчислень за таблицею Р. Фішера (дод. 9).

Для нашого прикладу табличне значення коефіцієнта кореляції при а = 0,05 і к = 8 становитиме г005 = 0,632.

Оскільки Гфакг > г005 (0,9344 > 0,632), можна підтвердити попередній висновок про те, що вибірковий коефіцієнт кореляції є вірогідним. Це дає підставу для висновку про дійсний зв'язок між продуктивністю корів і рівнем годівлі в генеральної сукупності.