Теорія статистики - Мармоза А.Т. - 10.2. Показники ряду динаміки

Одним з важливих завдань аналізу рядів динаміки є вивчення особливостей розвитку досліджуваних явищ за окремі періоди. Для виявлення напрямку та інтенсивності змін досліджуваних суспільних явищ за певні періоди часу визначають систему абсолютних і відносних показників динаміки. До таких показників відносяться абсолютний приріст, темп (коефіцієнт) зростання, темп приросту, абсолютне значення одного процента приросту і середні показники ряду динаміки (середній рівень ряду динаміки, середній абсолютний приріст, середній темп зростання і приросту та ін.).

Показники абсолютного приросту, темпу зростання і приросту, а також абсолютного значення одного процента приросту отримують порівнюючи між собою вихідні рівні ряду динаміки. При цьому рівень, з яким порівнюють, називають базисним,а порівнювальний - поточним рівнем.

Якщо порівнянню підлягають декілька послідовних рівнів, то можливі два варіанти порівняння:

1) кожен рівень вихідного ряду динаміки зіставляють з одним і тим самим рівнем, взятим за базу порівняння. Найчастіше за базу порівняння береться або початковий (перший) рівень, або ж рівень, з якого починається якийсь новий етап розвитку явища. Вибір бази порівняння повинен бути обґрунтований історично і економічно. Таке порівняння дістало назву порівняння з постійною базою;

2) кожен рівень вихідного ряду динаміки порівнюють з безпосередньо йому попереднім рівнем. Таке порівняння .називають порівнянням зі змінною базою.

Відповідно до цих двох варіантів порівняння отримують дві системи показників ряду динаміки. При порівнянні кожного рівня з одним і тим самим рівнем, взятим за базу порівняння, одержують базисні показники; при порівнянні кожного рівня з безпосередньо йому попереднім рівнем отримують ланцюгові показники.

Для характеристики абсолютної швидкості зростання (зниження) рівнів ряду динаміки обчислюють показник абсолютного приросту (А).

Абсолютний приріст являє собою різницю між двома рівнями, один з яких взято за базу порівняння.

Він показує, на скільки одиниць кожен даний рівень відрізняється від

рівня, взятого за базу порівняння. Абсолютний приріст може мати додатний або від'ємний знак. Якщо наступний рівень ряду динаміки більший за попередній, то абсолютний приріст буде мати знак "плюс", якщо менше - знак "мінус".

Динамічний ряд абсолютних приростів дає змогу визначити напрям (зростання, зниження) динаміки досліджуваного явища. Крім того, порівнянням абсолютних приростів між собою можна встановити характер зростання або зниження в абсолютному вираженні (рівномірний, прискорений, стрибкоподібний та ін.).

Розглянемо порядок обчислення абсолютних приростів та інших показників динаміки за даними про динаміку поголів'я корів в господарствах району за 2005-2010 рр. (табл. 10.3).

Абсолютні прирости становитимуть:

базисні (до 2005 р.)

Аі = уі -уо = 16875 - 16200 = 675 гол.;

А = у2 - Уо = 17121 - 16200 = 921 гол. і т. д.;

ланцюгові (до попереднього року)

А1 = у! - уо = 16875 - 16200 = 675 гол.;

А2 = у2 - уі = 17121 - 16875 = 246 гол. і т.д.;

Таблиця 10.3. Показники динаміки поголів'я корів в господарствах району за 2005 - 2010 рр.

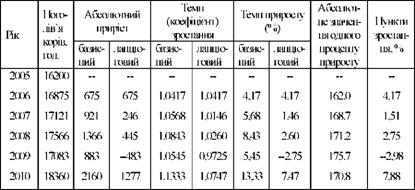
Ланцюгові і базисні абсолютні прирости пов'язані між собою такою рівністю: сума ланцюгових приростів дорівнює відповідному базисному приросту, тобто загальному приросту за весь відповідний період часу.

Для даного прикладу:

2160 = 675 + 246 + 445 + (- 483) + 1277.

Темп (коефіцієнт) зростання (К) - це відношення двох рівнів, один з яких взято за базу порівняння.

Темп зростання характеризує відносну швидкість зміни явища і показує у скільки разів кожний даний рівень більший або менший рівня, який взято за базу порівняння. Він може бути виражений у вигляді коефіцієнтів або процентів. Темп зростання, виражений у процентах, називають процентом зростання.

Величина темпу зростання буде більшою від одиниці, якщо рівень щодо бази порівняння зростає, і меншою за одиницю, якщо рівень щодо бази порівняння зменшується.

Темпи (коефіцієнти) зростання для нашого прикладу становитимуть:

базисні: к1 = Уі: у0 = 16875:16200 = 1,0417;

К2 = У2: Уо = 17121:16200 = 1,0568 і т.д.; ланцюгові: К1 = у1: у0 = 16875:16200 = 1,0417;

К2 = у2: Уі = 17121:16875 = 1,0146 і т.д. Між ланцюговими і базисними темпами зростання, вираженими коефіцієнтами, є такий взаємозв'язок:

а) добуток ланцюгових коефіцієнтів зростання дорівнює базисному коефіцієнту зростання за відповідний період. Наприклад:

ту ту ту - _

Для нашого прикладу

1,1333 = 1,0417 o 1,0146 o 1,0260 o 0,9725 o 1,0747.

б) частка від ділення двох сусідніх базисних коефіцієнтів зростання дорівнює відповідному ланцюговому коефіцієнту зростання.

Наприклад, К2 : К1 = : =

У" У 0 Л

Цей взаємозв'язок дає змогу здійснювати перехід від ланцюгових коефіцієнтів зростання до базисних і навпаки. Для нашого прикладу:

К2 = 1,0568:1,0417 = 1,0146; К3 = 1,0843: 1,0568 = 1,0260 і т.д.

Поряд з темпами зростання відносна зміна явища у часі може бути також охарактеризована за допомогою темпів приросту які являють собою відношення абсолютного приросту до рівня, взятого за базу порівняння (Т).

Темп приросту, як і абсолютний приріст може бути як додатним, так і від'ємним числом (відповідно при зростанні і зниженні рівня) і виражається у вигляді коефіцієнтів або процентів. На практиці темпи приросту найчастіше виражаються у формі процентів.

Вони показують наскільки процентів збільшився або зменшився поточний рівень порівняно з базисним, взятим за 100%.

Визначимо для нашого прикладу темпи приросту (в %): Т = (4 : у0)-100% = (675 : 16200)-100 = 4,17;

базисні:

Тг = (Аг: у0) -100% = (921:16200) -100 = 5,68 і т.д Т1 = (А1 : у0) -100% = (675:16200) -100 = 4,17;

ланцюгові

Тг = (Аг: у0)-100% = (246:16875)-100 = 1,46 і т . д.

Між темпом зростання і темпом приросту існує такий зв'язок:

або

Ті = (Кі -100%) -100%, тобто темп приросту завжди на одиницю менше відповідного темпу зростання, вираженого у формі коефіцієнта, або на 100%, якщо його виражено в процентах.

Отже, щоб визначити темп приросту, потрібно від темпу зростання відняти одиницю, якщо його виражено коефіцієнтом, або 100%, коли він у процентах.

Для динамічного ряду поголів'я корів темпи приросту, розраховані цим способом, становитимуть:

Т1 = А; o 100% - 100% = 1,0417-100% - 100% = 4,17%;

Т2 = А; o 100% - 1005 = 1,0568-100% - 100% = 5,68% і т.д.

Поряд з показниками темпів зростання і приросту в аналізі динамічних рядів викликає інтерес ще один відносний показник, який дає змогу визначити вагомість кожного процента приросту, і те, яка абсолютна величина приховується за цим процентом. Таким показником є абсолютне значення одного процента приросту (П). Він обчислюється як відношення абсолютного приросту до відповідного темпу приросту, вираженого в процентах

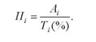
Розрахунок цього показника має економічний зміст тільки на ланцюговій основі, оскільки на базисній основі по всіх часових відрізках буде отримано одне і те саме значення показника - сота частина початкового (першого) рівня.

Абсолютне значення одного процента приросту для нашого прикладу становитиме:

Цей показник можна обчислити значно простіше. Підставивши у формулу значення відповідних показників, дістанемо, що величина абсолютного значення одного процента приросту являє собою соту частину попереднього рівня:

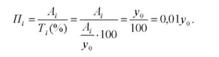
Таким чином, не вдаваючись до спеціального розрахунку, можна визначити, що абсолютне значення одного процента приросту для відповідних часових відрізків становитиме:

П = у0 : 100 = 16200 : 100 = 162,0 гол.;

П2 = уі : 100 = 16875 : 100 = 168,7 гол. і т.д.

Цей показник має важливе практичне значення в економічному аналізі, оскільки темпи зростання можуть сповільнюватись або залишатися на одному рівні, а абсолютне значення одного процента приросту зростати. Звичайно така закономірність спостерігається в динамічних рядах з рівнями, що постійно зростають.

Слід відмітити, що в динамічних рядах відносних величин (процентів зростання і приросту) їх безпосереднє порівняння можна здійснювати тільки шляхом визначення різниці рівнів. Ці різниці дістали назву пунктів зростання. їх розраховують як різницю базисних процентів зростання або приросту двох суміжних періодів. На відміну від темпів приросту, які не можна підсумовувати та перемножувати, пункти зростання можна підсумовувати, в результаті чого дістанемо темп приросту відповідного періоду порівняно з базисним періодом.

Пункти зростання для нашого прикладу становитимуть:

для 2007 р. ІГР1 = Т2 - Т1 = 5,68 - 4,17 = 1,51%;

для 2008 р. ПР2 = Т3 - Т2 = 8,43 - 5,88 = 2,75% і т.д.

Контроль правильності розрахунків: сума пунктів зростання дорівнює загальному темпу приросту за весь період:

4,17 + 1,51 + 2,75 + (- 2,98) + 7,88 = 13,33%.

Це відповідає темпу приросту рівня 2010 р. порівняно з 2005 р.

Для отримання узагальнюючих показників динаміки соціально-економічних явищ визначаються різного роду середні величини: середній рівень динамічного ряду, середній абсолютний приріст, середній темп зростання і приросту та ін. Середню з рівнів динамічного ряду називають хронологічною середньою. Середній рівень ряду динаміки характеризує типовий розмір рівнів ряду.

Порядок розрахунку середнього рівня для інтервальних і моментних рядів динаміки відрізняється. В інтервальних рядах динаміки з рівновіддаленими один від одного рівнями середній рівень обчислюється за формулою середньої арифметичної простої:

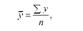
де п - число рівнів ряду динаміки.

Середній рівень динамічного ряду для нашого прикладу (табл. 10.3) становитиме:

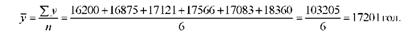
Якщо інтервальний ряд динаміки має нерівновіддалені один від одного рівні, то середній рівень розраховується за формулою середньої арифметичної зваженої:

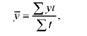
де і - відрізок часу, протягом якого зберігалося дане значення рівня у.

Наприклад, середня чисельність працівників агрофірми за перше півріччя становила 500 чоловік, за третій квартал - 520,а четвертий - 515 чоловік. Звідси середньорічна чисельність працівників становитиме:

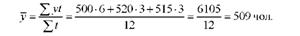
У моментних динамічних рядах з рівними проміжками між датами середній рівень обчислюється за формулою:

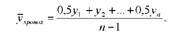
де п - число рівнів ряду динаміки.

Застосування формули проілюструємо на даних про спискову чисельність працівників підприємства за 2010 р. (табл. 10.4). Середньорічна чисельність працівників підприємства становитиме:

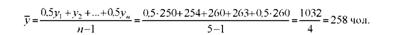
У моментних динамічних рядах з нерівними проміжками між датами середній рівень розраховують за формулою середньої арифметичної зваженої, тобто шляхом зваження рівнів за кількістю рівних періодів:

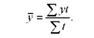
Порядок обчислення середнього рівня для моментного ряду динаміки показано в табл. 10.4.

Таблиця 10.4. Динаміка чисельності працівників підприємства в липні 2010 р.

Отже, середня чисельність працівників підприємства в липні 2010 р. становитиме:

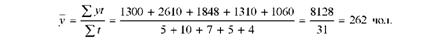
Середній абсолютний приріст характеризує середню швидкість зростання (або зниження) рівня. Для моментних та інтервальних рядів динаміки з рівними проміжками між датами його обчислюють як середню арифметичну просту з ланцюгових абсолютних приростів або як різницю між кінцевим і початковим рівнем, поділену на кількість членів ряду, зменшених на одиницю:

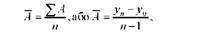
де п - число абсолютних приростів;

п - 1 - кількість рівнів ряду динаміки, зменшених на одиницю.

Середній абсолютний приріст для ряду динаміки поголів'я корів (табл. 10.3) становитиме:

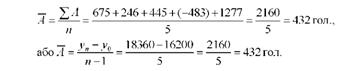
Для узагальнюючої характеристики темпів зростання за ряд років обчислюють середній темп (коефіцієнт) зростання (К). Він показує в скільки разів у середньому кожен даний рівень ряду більший (або менший) від попереднього рівня. Для динамічних рядів з рівними проміжками між датами середній темп зростання обчислюється за формулою середньої геометричної:

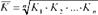
де К - коефіцієнти зростання на окремі періоди часу; п - число коефіцієнтів зростання.

Середній коефіцієнт зростання може бути визначений за іншою формулою, що випливає з наведеної вище формули:

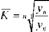
де п - число рівнів ряду динаміки;

Уо і уп - початковий і кінцевий рівні ряду динаміки

На основі середнього темпу зростання можна визначити середній темп приросту (Т ). Він показує, на скільки процентів у середньому збільшується (або зменшується) даний рівень порівняно з попереднім. Його розраховують як різницю між середнім темпом зростання, вираженим у процентах і 100%:

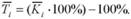
За даними табл. 10.3 розрахуємо середній коефіцієнт зростання поголів'я корів за 2005 - 2010 рр. Для цього використаємо формулу середньої геометричної

За таблицями антилогаріфмів знайдемо середній коефіцієнт зростання: К = 1,025, або 102,5%.

Такий самий результат дістанемо і за іншою (зручнішою) формулою, що випливає із взаємозв'язку ланцюгових і базисних коефіцієнтів: добуток ланцюгових коефіцієнтів дорівнює базисному крайніх періодів

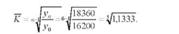
Прологарифмуємо рівняння:

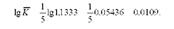
За таблицями антилогаріфмів знайдемо середній коефіцієнт зростання: К = 1,025, або 102,5%.

Такий самий результат матимемо і за іншою формулою:

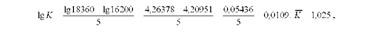
або 102,5%.

Обчисливши систему показників по ряду динаміки поголів'я корів (табл. 10.3). можна зробити такі висновки. Досліджуваний ряд динаміки є інтервальним. Середнє поголів'я корів за рік в господарствах району становить 17201 гол. Щорічно воно зростало в середньому на 432 голови. У цілому ж поголів'я корів за досліджуваний період (2005 - 2010 рр.) в районі зросло на 2160 гол., або на 13,33%. За середнім коефіцієнтом зростання можна встановити, що середній щорічний темп зростання поголів'я корів становить 2,5% (102,5 - 100). Із зростанням поголів'я корів збільшувалося абсолютне значення одного процента приросту з 162,0 гол. в 2006 р до 170,8 гол. в 2010 р.

При порівняльному аналізі кількох рядів динаміки, що відображають різні економічні явища за однакові відрізки часу, визначають коефіцієнт випередження. Він показує, у скільки разів швидше зростає рівень одного динамічного ряду (г) порівняно з другим (/), тобто

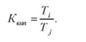
Наприклад, при порівнянні темпів зростання продуктивності праці і заробітної плати, урожайності і посівних площ, продуктивності тварин і їхньої чисельності тощо.

Так, якщо за п'ятиріччя (2005 - 2010 рр.) базисний темп зростання продуктивності праці в господарствах району становив Т,- = 115,6%, а темп зростання заробітної плати - Т, = 108,7%, коефіцієнт випередження темпу зростання продуктивності праці над темпом зростання заробітної плати дорівнює: Квип = І, : Т,- = 115,6 : 107,7 = 1,063, тобто темп зростання продуктивності праці випереджав тем зростання заробітної плати в 1,063 раза.