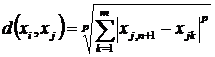Метод багатовимірних порівнянь набув широкого застосування в підведенні підсумків роботи, оцінці виконання плану, фінансового стану суб'єктів господарювання та їх підрозділів. Використання цього методу пов'язане зі складністю досліджуваних економічних явищ і процесів, їх багатогранністю та неоднозначністю. У цих умовах дати цілісну оцінку вказаних явищ за допомогою одного показника неможливо. Тому використовується система різнойменних показників.
Для приведення їх до однієї основи з подальшим об'єднанням в інтегральний показник використовується прийом стандартизації, який зводиться до перерахунку всіх показників в єдину стандартну форму. При цьому індивідуальні значення показників замінюються на відносні величини, ранги, бали, стандартні відхилення та ін.
Слід зазначити, що показники поділяються на стимулятори і дестимулятори. Стимулятори – це показники, збільшення яких покращує загальну оцінку роботи об'єкта дослідження (випуск продукції, продуктивність праці), а дестимулятори навпаки спричиняють погіршення оцінки роботи (собівартість, рекламації, брак, штрафи). Для приведення їх до однієї основи, однозначної характеристики показники-де-стимулятори обчислюються як обернена величина (продукція без рекламацій та ін.) або їх значення беруть зі знаком мінус.
В економічному аналізі використовується дві групи методів комплексної оцінки – детерміновані та стохастичні. До першої групи належать такі основні методи: метод сум, геометричної середньої, метод суми місць, метод відстаней.
Метод сум полягає у розрахунку загального інтегрального показника як суми його фактичних значень, виражених в абсолютних або відносних величинах.
Для підсумовування абсолютних показників застосовують формулу
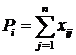 .
.
Із відносних показників інтегральний показник визначається так:
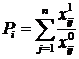 .
.
де 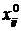 ,
, 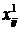 – базове та фактичне значення і-го показника на j-му об'єкті, і = 1, 2,..., n.
– базове та фактичне значення і-го показника на j-му об'єкті, і = 1, 2,..., n.
Метод сум використовується тоді, коли має місце односпрямованість досліджуваних показників (стимулятори або дестимулятори).
Недосконалістю інтегрального показника, розрахованого методом сум, є нівелювання низьких значень величин за рахунок перекриття їх іншими, вищими, показниками. Тобто, може бути висока інтегральна оцінка при надто низьких рівнях часткових показників. Крім того, не враховується значимість показників. Для усунення останнього недоліку можна додатково ввести вагові коефіцієнти d., які здебільшого визначаються експертним шляхом і дозволяють диференціювати відібрані показники за рівнем їх важливості:
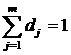
Після цього комплексний показник можна розрахувати за формулою
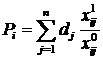
Приклад. Методом сум визначити найкращі підприємства харчової промисловості серед інших однотипних підприємств звичайним способом та з урахуванням рівня важливості показників (табл. 10.37).
Таблиця 10.37 показує, що ваговий коефіцієнт дозволяє зробити точніше порівняння з урахуванням важливості показників.
Метод суми місць полягає у попередньому розподілі кожного показника досліджуваних об'єктів за місцями серед інших однойменних показників з наступним їх додаванням для визначенням кращих об'єктів.
Для цього застосовують ранжування визначеної суми місць. Критерій оцінки найкращого об'єкта – мінімальна сума місць, бо чим менша сума місць, тим кращі результати роботи.
Може виникнути ситуація, коли за розрахованою сумою місць кілька досліджуваних об'єктів порівняльного аналізу претендують на одне і те саме місце. Першість буде мати той із них, хто при підрахунку суми місць набере більше додатних і менше від'ємних значень.
Приклад. Методом суми місць визначити найкращі підприємства харчової промисловості серед інших однотипних підприємств (табл. 10.38).
Слід звернути увагу та те, що чотири підприємства (G та І; D та Н) набрали однакову суму місць – відповідно по 14 і 23. Щоб розділити зайняті ними місця, доцільно підрахувати і порівняти суму додатних і від'ємних відхилень показників. У якого з них будуть кращі показники, те підприємство і займе вище місце:
Для підприємства G:
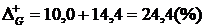 ;
; 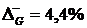 ,
, 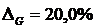
Для підприємства І:
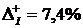 ;
; 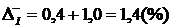 ,
, 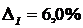
Таким чином, третє місце належатиме підприємству G, а четверте – підприємству І.
Таблиця 10.37. Комплексна оцінка діяльності підприємств методом сум
Підприємство | Виконання плану,% | Сума показників | Місце | 3 урахуванням значущості показників | ||||
випуск продукції | продуктивність праці | собівартість | ||||||
сума показників | місце | |||||||
№ з/п | 1 | 2 | 3 | 4=1+2-3 | 5 | 6 = 1ž3 + 2ž2-3ž1 | 7 | |
А | 123,4 | 115,4 | 104,6 | 134,2 | 2 | 496,4 | 2 | |
В | 100,6 | 98,5 | 91,3 | 107,8 | 4 | 407,5 | 7 | |
С | 140,1 | 114,9 | 107,2 | 147,8 | 1 | 542,9 | 1 | |
D | 98,3 | 98,7 | 112,3 | 84,7 | 9 | 380,0 | 6 | |
Б | 87,5 | 95,3 | 94,5 | 88,3 | 7 | 358,6 | 9 | |
F | 114,8 | 101,5 | 110,3 | 106,0 | 6 | 437,1 | 3 | |
G | 110,0 | 95,6 | 85,6 | 120,0 | 3 | 435,6 | 5 | |
Н | 85,4 | 102,5 | 113,8 | 74,1 | 10 | 347,4 | 8 | |
І | 99,6 | 107,4 | 100,0 | 107,0 | 5 | 413,6 | 4 | |
J | 82,4 | 99,4 | 95,6 | 86,2 | 8 | 350,4 | 10 | |
Коефіцієнт значущості | 3 | 2 | 1 | – | – | |||
Стимулятор "+1" дестимулятор "–1" | +1 | +1 | -1 | |||||
Підприємство | Виконання плану,% | Сума місць | Отримане місце | |||||
випуск продукції | продуктивність праці | собівартість | ||||||
% | місце | % | місце | % | місце | |||
№ з/п | 1 | 2 | 3 | 4 | 5 | 6 | 7= 2 + 4 + 6 | 8 |
А | 123,4 | 2 | 115,4 | 1 | 104,6 | 6 | 9 | 1 |
В | 100,6 | 5 | 98,5 | 8 | 91,3 | 2 | 15 | 5 |
С | 140,1 | 1 | 114,9 | 2 | 107,2 | 7 | 10 | 2 |
D | 98,3 | 7 | 98,7 | 7 | 112,3 | 9 | 23 | 9 |
Б | 87,5 | 8 | 95,3 | 10 | 94,5 | 3 | 21 | 8 |
F | 114,8 | 3 | 101,5 | 5 | 110,3 | 8 | 16 | 6 |
G | 110,0 | 4 | 95,6 | 9 | 85,6 | 1 | 14 | 3 |
Н | 85,4 | 9 | 102,5 | 4 | 113,8 | 10 | 23 | 10 |
І | 99,6 | 6 | 107,4 | 3 | 101,0 | 5 | 14 | 4 |
J | 82,4 | 10 | 99,4 | 6 | 95,6 | 4 | 20 | 7 |
Аналогічно робляться розрахунки по підприємствах D та Н, в результаті чого підприємство D займе дев'яте, а підприємство Н – десяте місця.
Метод коефіцієнтів передбачає визначення загального інтегрального показника у вигляді добутку відповідних часткових коефіцієнтів, які показують відносну зміну досліджуваних показників:
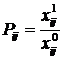
Для визначення добутку показників використовують таку формулу:
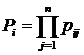 ,
, 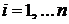 .
.
Приклад. Методом коефіцієнтів визначити найкращі промислові підприємства серед інших однотипних підприємств (табл. 10.39).
Дані таблиці свідчать, що за комплексним показником перше місце зайняло підприємство С, друге – А і т. п.
Метод геометричної середньої передбачає визначення комплексної оцінки за допомогою розрахунку середньої геометричної із коефіцієнтів відносної зміни досліджуваних показників. Для цього використовується формула
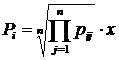
Проте слід пам'ятати, що цей метод використовується тоді, коли найбільший показник не перевищує одиниці, а всі інші наближені до неї, тобто 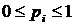 .
.
Метод відстаней – метод комплексної оцінки, який полягає в оцінці результатів діяльності порівняно з еталоном, до якого прагне підприємство. Він ґрунтується на визначенні ступеня близькості об'єктів, які вивчаються, до об'єкта, що виступає в ролі еталона.
Підприємство | Коефіцієнти виконання планового завдання | Добуток показників | Отримане місце | ||
Випуск продукції | Продуктивність праці | Прибуток | |||
№ з/п | 1 | 2 | 3 | 4 = 1-2-3 | 5 |
А | 1,23 | 1,15 | 1,15 | 1,63 | 2 |
В | 1,01 | 0,99 | 0,99 | 0,98 | 7 |
С | 1,40 | 1,15 | 1,05 | 1,70 | 1 |
D | 0,98 | 1,00 | 1Д4 | 1,12 | 4 |
Е | 0,88 | 0,95 | 0,97 | 0,80 | 9 |
F | 1,15 | 1,02 | 1,20 | 1,40 | 3 |
G | 1,10 | 0,96 | 0,86 | 0,90 | 8 |
Н | 0,85 | 1,03 | 1,27 | 1,11 | 5 |
І | 1,00 | 1,06 | 1,02 | 1,07 | 6 |
J | 0,82 | 0,99 | 0,95 | 0,77 | 10 |
При цьому еталонний об'єкт (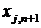 ) визначається з однотипних підприємств однієї або різних галузей. Він має умовний характер і відображає максимальні чи середні значення усіх показників, тобто:
) визначається з однотипних підприємств однієї або різних галузей. Він має умовний характер і відображає максимальні чи середні значення усіх показників, тобто:
 ,
,
або
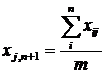
де і = 1, 2,..., n; j = 1, 2, ...m.
У випадках, коли відхилення у виконанні плану не бажане, за еталон приймається підприємство зі 100%-м виконанням плану.
У практиці порівняльного аналізу найчастіше застосовуються такі функції відстані, які подано в табл. 10.40.
Таблиця 10.40. Основні функції відстані в багатовимірному аналізі
Назва функції | Формула розрахунку |
Евклідова відстань |
|
Зважена евклідова відстань |
|
|
|
|
|
Якщо одиниці виміру показників, які використовуються при визначенні відстані, різнорідні і непорівнянні, тоді вони приводяться до стандартного вигляду шляхом ділення значень цих показників на еталонний показник:
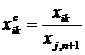
де 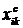 – стандартизовані показники стану k-то об'єкта;
– стандартизовані показники стану k-то об'єкта;
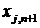 – показник еталонного (умовного) об'єкта;
– показник еталонного (умовного) об'єкта;
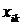 – вихідні дані.
– вихідні дані.
Впорядкування (ранжування) об'єктів аналізу проводиться в порядку зменшення комплексної оцінки.
Приклад. Діяльність виробничих підрозділів підприємства характеризується даними, що наведені в табл. 10.41. Дати комплексну оцінку діяльності виробничих підрозділів за методом відстаней.
Спочатку сформуємо умовне підприємство – еталон, вибравши для цього найвищі рівні виконання плану за кожним показником і виробничим підрозділом. Для зручності розрахунків занесемо ці дані у вихідну таблицю окремим рядком.
Для розрахунків використаємо найпростішу функцію Іх – норма. В результаті отримаємо дані, наведені в табл. 10.42.
Розв'яжемо цю саму задачу методом Евклідової відстані. Для визначення та ранжування підприємств за показником наближення виконання плану до еталону, необхідно розрахувати показники координації, що відображено в табл. 10.43.
Аналогічно розраховуються інші показники таблиці.
Розрахунок показників проводиться шляхом відношення порівнюваного показника до умовного підприємства-еталону, тобто: по групі цехів за показником випуску продукції:
Вплану №1 = 105.61 : 105,61 = 1,000;
Вплану №1 = 103.8 :105,61 = 0,983;
Вплану №1 = 99.3 : 105,61 = 0,940;
Вплану №1 = 101.6:105,61 = 0,962.
Потім розраховується показник комплексної оцінки за формулою
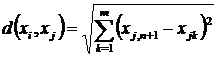
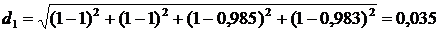 ;
;
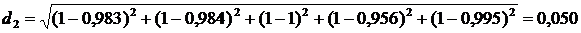 ;
;
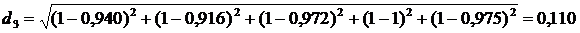 ;
;
 .
.
Цех | Виконання плану,% | ||||
випуск продукції | прибуток | договори постачання | продуктивність праці | зниження собівартості | |
А | 1 | 2 | 3 | 4 | 5 |
№1 | 105,6 | 105,2 | 98,2 | 104,5 | 101,3 |
№2 | 103,8 | 103,5 | 99,5 | 102,6 | 102,6 |
№3 | 99,3 | 96,4 | 96,7 | 107,3 | 100,5 |
№4 | 101,6 | 98,7 | 97,3 | 104,9 | 103,1 |
Еталон № 1 (максимальні значення) | 105,6 | 105,2 | 99,5 | 107,3 | 103,1 |
Еталон № 2 (середні значення) | 102,6 | 101,0 | 97,9 | 104,8 | 101,9 |
Таблиця 10.42. Комплексна оцінка діяльності цехів методом відстаней (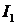 -норма)
-норма)
Цех | Абсолютні відхилення рівня виконання плану від еталону,% | Місце | |||||
випуск продукції | прибуток | договори постачання | продуктивність праці | зниження собівартості | сума | ||
Еталон № 1 – максимальні значення показників | |||||||
№1 | 0,0 | 0,0 | -1,3 | -2,8 | -1,8 | -5,9 | 1 |
№2 | -1,8 | -1,7 | 0,0 | -4,7 | -0,5 | -8,7 | 2 |
№3 | -6,3 | -8,8 | -2,8 | 0,0 | -2,6 | -20,5 | 4 |
№4 | -4 | -6,5 | -2,2 | -2,4 | 0,0 | -15,1 | 3 |
Еталон № 2 – середні значення показників | |||||||
№1 | 3,0 | 4,2 | 0,3 | -0,3 | -0,6 | 6,6 | 3 |
№2 | 1,2 | 2,5 | 1,6 | -2,2 | 0,7 | 3,8 | 2 |
№3 | -3,3 | -4,6 | -1,2 | 2,5 | -1,4 | -8,0 | 4 |
№4 | "1,0 | -2,3 | -0,6 | 0,1 | 1,2 | -2,6 | 1 |
Таблиця 10.43. Комплексна оцінка діяльності цехів методом відстаней (Евклідова відстань)
Цех | Показники координації рівня виконання плану до еталону | Місце | |||||
випуск продукції | прибуток | договори постачання | продуктивність праці | зниження собівартості | показник комплексної оцінки | ||
Еталон № 1 – максимальні значення показників | |||||||
№ 1 | 1,000 | 1,000 | 0,985 | 0,974 | 0,983 | 0,035 | 1 |
№2 | 0,983 | 0,984 | 1,000 | 0,956 | 0,995 | 0,050 | 2 |
№3 | 0,940 | 0,916 | 0,972 | 1,000 | 0,975 | 0,110 | 4 |
№4 | 0,962 | 0,937 | 0,978 | 0,978 | 1,000 | 0,080 | 3 |
Цехи ранжуються в порядку зменшення комплексної оцінки, тому що найменше віддалення від еталону означає найвище значення рейтингової оцінки.
Аналогічно можна зробити розрахунки за еталоном № 2.
Крім розглянутих та інших детермінованих методів комплексної оцінки при порівнянні діяльності підприємств використовуються методи стохастичної комплексної оцінки. Вони призначені для дослідження стохастичного зв'язку і включають методи компонентного аналізу, двовимірного шкалування, багатовимірного факторного аналізу, експертно-статистичні та ін.
Віддаючи належну увагу методам багатовимірних порівнянь, аналітики разом з тим зазначають, що розраховуючи показник комплексної (інтегральної) оцінки, треба пам'ятати про те, що він є лише операційним поняттям, не має самостійного економічного змісту. Тому він має право на існування лише на практиці порівняльного аналізу з метою ранжування об'єктів і прийняття рішень. Недоліками методів багатовимірних порівнянь є складність у розрахунках, недостатня наочність і суперечливість, оскільки величини з більшою варіацією матимуть вищу вагу в інтегральному показнику, завдяки чому вони отримують перевагу порівняно з іншими показниками.
Розділ 11. МЕТОДИ ДЕТЕРМІНОВАНОГО ФАКТОРНОГО АНАЛІЗУ
11.1. Індексний метод
11.2. Метод різниць
11.3. Інтегральний метод
11.4. Методи пропорційного ділення та часткової участі
11.5. Метод логарифмування
НАВЧАЛЬНИЙ ТРЕНІНГ
Розділ 12. МЕТОДИ СТОХАСТИЧНОГО ФАКТОРНОГО АНАЛІЗУ
12.1. Дисперсійний аналіз
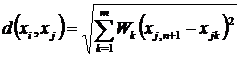
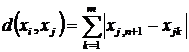
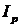 – норма
– норма