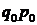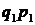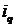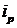Теорія економічного аналізу - Купалова Г.І. - Розділ 11. МЕТОДИ ДЕТЕРМІНОВАНОГО ФАКТОРНОГО АНАЛІЗУ

11.1. Індексний метод.

11.2. Метод різниць.

11.3. Інтегральний метод.

11.4. Методи пропорційного ділення та часткової участі.

11.5. Метод логарифмування.

Навчальний тренінг.

Детермінований факторний аналіз, тобто аналіз залежностей між показниками за допомогою жорстко детермінованих факторних систем, є найбільш поширеним видом аналізу в господарській практиці. Методи детермінованого факторного аналізу призначені для виміру впливу факторів на результативний показник. До цих методів належать: індексний, різниць, інтегральний, пропорційного ділення, логарифмування та ін. В основу перших двох методів покладено прийом елімінування.

Елімінування (лат. eliminate – виключати, усувати) полягає у послідовному визначенні впливу кожного фактора на результативний показник за умови незмінності інших факторів та абстрагування їх взаємного впливу.

Розглянемо детальніше основні методи детермінованого факторного аналізу.

11.1. Індексний метод

Індексний метод є одним із найбільш потужних, інформативних і поширених інструментів економічного аналізу на всіх його рівнях, починаючи від аналізу окремих суб'єктів господарювання до макроекономічних досліджень національної економіки. Така велика роль індексів пояснюється тим, що вони дають змогу аналізувати зміну явища у часі, просторі, оцінювати рівень виконання планового завдання, а також дають змогу вивчати взаємозв'язки і виявляти та вимірювати вплив факторів на зміну складних явищ.

Використовуючи індексний метод, можна охарактеризувати зміну найрізноманітніших економічних показників у часі та в просторі: обсягів виробленої продукції, виробничих потужностей, посівних площ, цін, вартості і собівартості продукції, продуктивності праці тощо. Особливо широкого застосування набув індексний метод в торгівлі. Тут обраховуються індекси обсягу та якісних показників, завдяки яким характеризуються зміни обсягів надходження та реалізації товарів, товарних запасів, цін, продуктивності праці, витрат, прибутку тощо. Розглянемо застосування індексного методу в аналізі на прикладі індексів товарообігу, ціни та фізичного обсягу.

Дослівно індекс (index) перекладається з латинської як "показник". Індекс – це відносна величина, за допомогою якої можна порівнювати окремі показники однорідного об'єкта та складні економічні явища, утворені з різнорідних елементів, що не підлягають безпосередньому підсумовуванню.

Індивідуальний індекс (простий, частковий) – це результат порівняння двох показників, які належать однорідному об'єкту (наприклад, цін якогось товару, обсягів його реалізації, кількості виробленої продукції у звітному і базисному періодах тощо).

В індивідуальних індексах досліджувана ознака береться без урахування зв'язку її з іншими ознаками явища, що вивчається. Наприклад, індивідуальний індекс ціни має вигляд

,

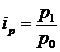а фізичного обсягу

,

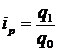де

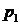– ціна одиниці товару у звітному періоді, грн;

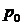– ціна одиниці товару у базисному періоді, грн;

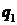– кількість проданих товарів у звітному періоді, од.;

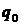– кількість проданих товарів у базисному періоді, од.

Зведений індекс (складний, аналітичний, агрегатний) виражає співвідношення складних соціально-економічних явищ, які складаються або з безпосередньо несумірних елементів, або окремих частин цих явищ. У першому випадку ми отримуємо загальний індекс, а в другому – груповий (субіндекс).

Отже, у зведених індексах досліджувана ознака береться не ізольовано, а у зв'язку з іншими ознаками. Зведений, або агрегатний індекс завжди складається із двох компонентів:

1) ознака, яка індексується, тобто динаміка якої вивчається;

2) су мірник, який називається вагою. За допомогою ознак-ваг вимірюється динаміка складного економічного явища, окремі елементи якого несумірні.

Для обчислення загальних індексів необхідно привести їх складові до сумірного вигляду. Наприклад, для оцінки зміни обсягу різнорідної продукції у двох порівнюваних періодах потрібно прийняти однакові ціни, а для оцінки зміни рівня цін на групу товарів слід зіставити однакові обсяги цих товарів. Специфіка індексного методу полягає у приведенні елементів складного явища до порівнянного вигляду. Ваги беруться однаковими в числівнику і знаменнику індексу. При цьому основою індексного методу, наприклад при визначенні змін у виробництві та обігу товарів, є перехід від натурально-речової форми вираження товарних мас до вартісних (грошових) вимірників. Саме через грошовий вираз вартості окремих товарів усувається їх непорівнянність і досягається єдність.

Розглянемо зведений індекс цін, який розраховується за формулою

.

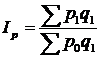З цієї формули видно, що індексована величина – ціна (р), а вагами виступає обсяг продукції звітного періоду (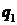). У чисельнику індексу – вартісний показник реального товарообігу звітного періоду, а в знаменнику – умовного товарообігу звітного періоду в цінах базисного періоду.

Різниця між чисельником і знаменником індексу цін відображає суму економії (або перевитрат) покупців від зниження (або підвищення) цін. Якщо різниця 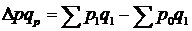позитивна, це означає перевитрати, якщо від'ємна – то економію для покупців.

Зведений індекс фізичного обсягу має такий вигляд:

.

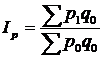В цьому індексі індексованою величиною виступає кількість товарів у натуральному вираженні, а вагами – ціни. Застосування зведеного індексу фізичного обсягу дає можливість оцінити зміну фізичного обсягу продаж при збереженні цін незмінними.

У зведеному індексі обсягу товарообігу зіставляються два вартісних показники – товарообороти звітного та базисного періодів. Він має вигляд:

.

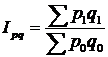В аналізі фінансово-господарської діяльності за допомогою індексів вирішуються такі завдання:

1) оцінка зміни рівня явища (або відносної зміни показника);

2) виявлення ролі окремих факторів у зміні результативної ознаки;

3) оцінка впливу зміни структури сукупності на динаміку (рис. 11.1).

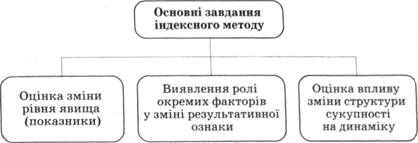
Рис. 11.1. Основні завдання індексного методу

Завдання 1. Аналіз та оцінка зміни рівня явища може здійснюватися:

– шляхом порівняння фактичних показників з плановими за допомогою індексу виконання плану: ;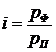

– за часом з використанням індексу зміни в динаміці: ;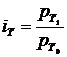

– у просторових порівняннях, наприклад у порівнянні з еталонним підприємством: .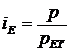

В аналізі динаміки використовуються базисні індекси (розраховані стосовно базисного періоду) і ланцюгові індекси (розраховані стосовно попереднього періоду).

Приклад. Розрахувати індивідуальні індекси цін, обсягу продажу і товарообігу. Визначити вплив факторів на зміну товарообігу у серпні порівняно з червнем за даними продажу овочів на базарах міста (табл. 11.1)

Індивідуальний індекс цін для огірків становитиме:

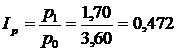, або 47,2%

Це означає, що ціна знизилася на 52,8%. Індивідуальний індекс фізичного обсягу реалізації огірків:

Таблиця 11.1. Ціна та обсяг продажу овочів на ринках міста

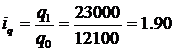, або 190%.

Приріст фізичного обсягу огірків – 90%. Індекс вартості товарообігу огірків дорівнює:

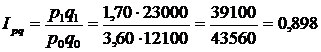, або 89,8%.

Тобто вартість товарообігу знизилася на 10,2%.

Завдання 2. Індексний аналіз за факторами – аналіз, мета якого полягає в оцінці ізольованого впливу окремих факторів на результат.

У багатофакторних моделях необхідно спочатку впорядкувати фактори за принципом первинності та вторинності, а потім послідовно їх замінювати. За допомогою зведених індексів можна, наприклад, визначити ступінь зміни товарообігу як в результаті змін індивідуальних цін на товари, так і в результаті зміни фізичного обсягу їх продажу. Проілюструємо це на наведеному нижче прикладі.

Для оцінки середньої зміни цін на овочі розрахуємо зведений індекс цін:

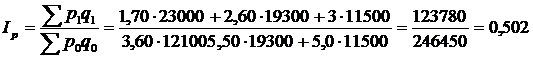, або 50,2%.

Отже, у серпні порівняно з червнем ціни на овочі в середньому знизилися на 49,8%. Це відповідно відобразилося на зміні вартості товарообігу (&pqp). Для визначення цієї зміни слід знайти різницю між чисельником і знаменником зведеного індексу ціни:

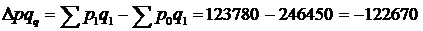(грн.).

Таким чином, вартість товарообігу овочів на базарах міста у серпні порівняно з червнем зменшилася через падіння цін на 122 670 грн. Оскільки отримана різниця від'ємна, то це означає, що населення зекономило на покупці овочів названу суму грошей.

Індекс фізичного обсягу реалізації для досліджуваної групи овочів дорівнює:

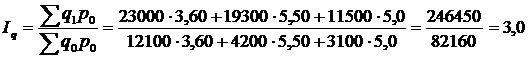, або 300,0%.

Фізичний обсяг реалізації овочів зріс у три рази, або на 200,0%. В абсолютному вираженні зміна вартості товарообігу під впливом зміни обсягу реалізації (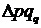) становить:

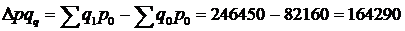(грн).

Індекс вартості товарообігу становитиме:

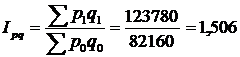, або 150,6%.

Це означає, що в результаті змін цін на товари і обсягу продажу овочів вартість товарообігу збільшилася на 50,6%, або на 123 780 - 82 160 = 41 620 (грн).

Прослідкуємо взаємозв'язок індексів:

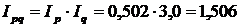, або 150,6%,

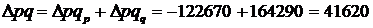(грн).

Висновок. У серпні місяці порівняно з червнем вартість товарообігу овочів на базарах міста збільшилася в 1,506 разу (на 50,6%), або на 41 620 грн. На це вплинуло два фактори: зміни цін та обсягу продажу. Так, через падіння цін товарообіг скоротився в 0,502 разу (на 49,8%), або на 122 670 грн, завдяки чому населення зекономило цю суму грошей на здійсненні покупок овочів. Проте завдяки збільшенню обсягу реалізації вартість товарообігу овочів збільшилася втричі (на 200%), або на 164 290 грн.

Слід пам'ятати, що при побудові зведених агрегатних індексів дотримуються таких правил:

– для індексів якісних показників (цін, собівартості, продуктивності праці, урожайності) ваги вибираються на рівні звітного періоду;

– для індексів об'ємних показників (фізичний обсяг реалізації, обсяг виробленої продукції, посівна площа) – ваги вибираються на рівні базисного періоду.

Зведений (агрегатний) індекс може бути перетворений в середній арифметичний і середній гармонічний індекси.

Зведений середній арифметичний індекс фізичного обсягу реалізації продукції застосовується, якщо відомі індивідуальні індекси фізичного обсягу і показники вартості товарообігу базисного періоду. Цей індекс розраховується за формулою

.

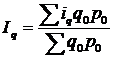Приклад. За наведеними даними розрахувати індекс фізичного обсягу реалізації (табл. 11.2):

Таблиця 11.2. Товарообіг та індивідуальні індекси цін, фізичного обсягу за видами товарів

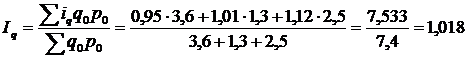, або 101,8%.

Отже, фізичний обсяг товарної групи зріс на 1,8%.

Середній гармонічний індекс – це середня гармонічна з індивідуальних індексів і розраховується в тих випадках, коли відсутні дані для розрахунку індексу цін в агрегатній формі. Він обчислюється за формулою

.

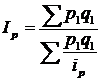У нашому прикладі:

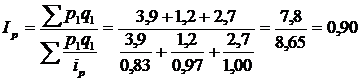, або 90%.

Таким чином, ціни в середньому знизилися на 10%.

Завдання 3. Аналіз структури сукупності та її оцінка здійснюється у таких випадках:

– при вивченні об'ємних показників чи явищ, які мають складну структуру (структура товарообігу, структура працівників за категоріями тощо). У таких умовах структурні зрушення впливають на зміну досліджуваного показника або явища;

– при аналізі середніх рівнів досліджуваних явищ (зміна частки працівників з вищою продуктивністю праці призводить до зміни середньої продуктивності праці).

Для відображення впливу змін у структурі досліджуваної сукупності на динаміку досліджуваного явища обчислюється індекс структури (структурних зрушень), величина якого дорівнює частці від ділення індексу змінного складу (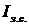) на індекс постійного, або, як його ще називають, фіксованого складу ():

.

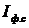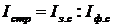Індексом постійного (фіксованого) складу називається індекс, в чисельнику і знаменнику якого ваги беруться (фіксуються) на рівні однакового періоду. Так, індекс цін фіксованого складу визначається за формулою

.

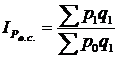Індекс змінного складу є співвідношенням середніх рівнів досліджуваного явища. Якщо індекс постійного (фіксованого) складу показує середню зміну лише однієї індексованої величини, то індекс змінного складу характеризує загальну зміну середньої як в результаті зміни індивідуальних значень величини, яка індексується, так і в результаті зміни структури сукупності (ваг). Індекс цін змінного складу визначається за формулою

.

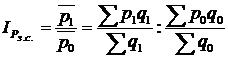Аналогічно розраховується індекс собівартості змінного складу та ін.

Приклад. Розрахувати вплив структурних зрушень на зміну середньої собівартості двох однотипних виробів за такими даними (табл. 11.3):

Таблиця 11.3. Собівартість та обсяги виробництва окремих видів продукції

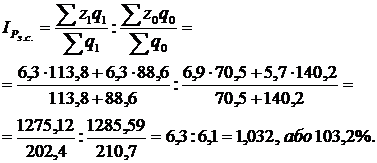
Під впливом зміни індивідуальних собівартостей і структурних зрушень у виробництві виробів середня собівартість збільшилася на 3,2%.

Індекс собівартості фіксованого складу дорівнює:

?

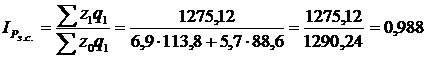або 98,8%.

Під впливом зміни індивідуальних собівартостей середня собівартість знизилася на 1,2%.

Тепер розрахуємо індекс структури:

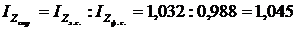, або 104,5%.

Індекс структури свідчить про збільшення собівартості продукції на 4,5% через зміну структури виробленої продукції.

Взаємозв'язок індексів (баланс відхилень):

.

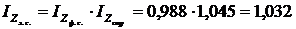Наявний також дещо інший детальніший спосіб розрахунків названих індексів, зокрема з урахуванням показника частки окремих видів продукції у її загальному обсязі. Для зручності побудуємо допоміжну таблицю, в якій покажемо необхідні розрахункові величини (табл. 11.4).

Визначення динаміки середньої собівартості одиниці виробів і впливу структурних зрушень в асортименті виробів проведемо за допомогою відповідних структурних коефіцієнтів та індексу структурних зрушень:

1) розрахуємо спочатку структурні коефіцієнти за виробами А і Б:

; ;

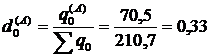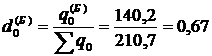Таблиця 11.4. Розрахункові дані для індексного аналізу витрат виробництва

; ;

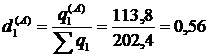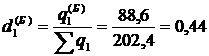2) побудуємо індекс собівартості змінного складу:

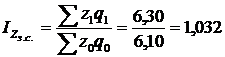, або 103,2%;

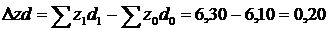(тис. грн.);

4) побудуємо індекс структурних зрушень:

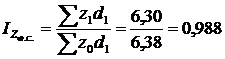, або 98,8%;

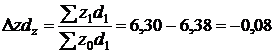(тис. грн);

Взаємозв'язок індексів (баланс відхилень):

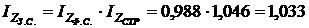, або 103,3%.

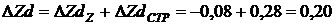(тис. грн).

Одержані результати індексного аналізу дають змогу зробити такі висновки:

– у звітному періоді порівняно з базовим загальні витрати на виробництво збільшилися на 3,2%, що у натуральному виразі склало 0,2 тис. грн;

– на зміну загальної суми витрат вплинули такі фактори:

• зміна собівартості виробів і структури;

• зміна собівартості виробу привела до зменшення витрат виробництва на 1,2%, що у натуральному виразі склало 0,07 тис. грн;

• зміна структури виробництва спричинила зростання витрат виробництва на 4,5% або на 0,27 тис. грн.

Віддаючи належне індексному методу в дослідженнях складних економічних явищ, слід вказати і на його недолік, а саме на те, що він призначений переважно для визначення впливу двох факторів у мультиплікативних моделях, що звужує сферу його застосування.