12.1. Дисперсний аналіз.
12.2. Регресійний аналіз.
12.3. Кореляційний аналіз.
12.4. Кластерний аналіз.
Навчальний тренінг.
Функціонування економіки України в ринковому середовищі потребує вивчення і врахування дії цілого комплексу взаємопов'язаних факторів для оперативного прийняття та реалізації зважених управлінських рішень. При цьому традиційних методів та методів детермінованого факторного аналізу вже недостатньо у зв'язку з обмеженістю їх аналітичних можливостей, недостатністю інформаційного забезпечення тощо. Тому виникає необхідність ширшого застосування методів стохастичного факторного аналізу, які, на відміну від жорстко регламентованих методів детермінованого аналізу, основаних на функціональній залежності результативного показника від факторних, дають змогу врахувати вплив сукупності факторів, що носять імовірнісний, невизначений характер.
До методів стохастичного факторного аналізу належать: дисперсійний, регресійний, кореляційний, компонентний, багатовимірний та інші види аналізу.
12.1. Дисперсійний аналіз
Дисперсія (лат. dispersio – розсіювання) часто застосовується в теорії ймовірностей і математичній статистиці. Означає ступінь розсіювання навколо середнього значення випадкової величини. У статистичному розумінні дисперсія є середнє арифметичне із квадратів відхилень величин від їх середнього арифметичного. На практиці при проведенні аналізу економічного стану підприємства чи галузі часто необхідно оцінити розсіювання можливих значень випадкової величини навколо її середнього значення, а також виявити та виміряти силу зв'язку між факторними та результативною ознаками.
Дисперсійний аналіз – це статистичний метод, призначений для встановлення структури зв'язку між результативною та факторними ознаками. Він дає змогу визначити вплив одного або декількох факторів на результативний показник.
Дисперсійний аналіз може застосовуватися за обмеженої кількості одиниць спостереження. До того ж він особливо ефективний в умовах, коли результативна ознака суттєво змінюється під одночасною дією кількох факторів з неоднаковою силою впливу.
Дисперсійний метод аналізу відіграє велику роль в економічних дослідженнях завдяки тому, що він має самостійне значення. Завдяки цьому методу вирішуються такі завдання:
– кількісне вимірювання сили впливу факторних ознак та їх сполучень на результативну;
– оцінка вірогідності впливу та його довірчих меж;
– аналіз окремих середніх і статистична оцінка їх різниці.
Крім того, у поглибленому аналізі дисперсійний метод може виконувати допоміжні функції, які дають змогу обґрунтовано використовувати інші методи аналізу.
Розв'язання задачі виміру зв'язку спирається на розкладення суми квадратів відхилень досліджуваних значень результативної ознаки від загальної середньої на окремі частини, які обумовлюють зміну цієї ознаки. Якщо сукупність розбита на групи, то при цьому розраховуються загальна, групова, середня з групових і міжгрупова дисперсії.
Загальна дисперсія (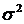 ) – це середній квадрат відхилень окремих значень ознак (х) від їх середньої величини. Вона обчислюється за формулою
) – це середній квадрат відхилень окремих значень ознак (х) від їх середньої величини. Вона обчислюється за формулою
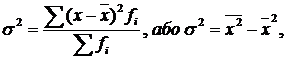
де 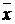 – загальна середня для всієї досліджуваної сукупності;
– загальна середня для всієї досліджуваної сукупності;
f – обсяг сукупності (кількість одиниць).
Загальна дисперсія відображає варіацію досліджуваної ознаки за рахунок усіх умов, які впливають на неї у цій сукупності.
Групова дисперсія (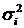 ) є середнім квадратом відхилень варіантів ознаки (х) від групової середньої величини. Розраховується за формулою
) є середнім квадратом відхилень варіантів ознаки (х) від групової середньої величини. Розраховується за формулою
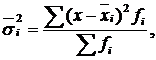
де 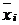 – групова середня;
– групова середня;
і – порядковий номер х та f в межах групи. Групова дисперсія характеризує варіацію ознаки в межах групи за рахунок всіх інших факторів за виключенням того, який покладений в основу групування.
Щоб виміряти таку варіацію для сукупності в цілому, необхідно знайти середню із групових дисперсій.
Середня з групових дисперсій (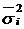 ) визначається за формулою
) визначається за формулою
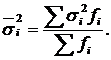
Середня з групових дисперсій характеризує випадкову варіацію в кожній окремій групі. Ця варіація виникає під впливом інших факторів, що не враховуються, і не залежить від ознаки-фактора, покладеної в основу групування.
Міжгрупова дисперсія (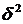 ) або дисперсія групових середніх вимірює варіацію результативної ознаки за рахунок факторної ознаки, покладеної в основу групування. Її формула
) або дисперсія групових середніх вимірює варіацію результативної ознаки за рахунок факторної ознаки, покладеної в основу групування. Її формула
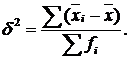
Приклад. За даними табл. 12.1 зробити дисперсійний аналіз варіації урожайності озимої пшениці за двома виробничими підрозділами. При цьому другий підрозділ вніс мінеральні добрива, а перший – ні.
Таблиця 12.1. Посівні площі та урожайність озимої пшениці в господарстві за двома виробничими підрозділами
Підрозділ № 1 (не вносив добрив) | |||||
1 | 50 | 20 | 1000 | 400 | 20 000 |
2 | 25 | 22 | 550 | 484 | 12 100 |
3 | 25 | 25 | 625 | 625 | 15 625 |
Разом | 100 | — | 2175 | 1509 | 47 725 |
Підрозділ № 2 (вносив добрива) | |||||
4 | 50 | 30 | 1500 | 900 | 45 000 |
5 | 75 | 35 | 2625 | 1225 | 91875 |
6 | 25 | 40 | 1000 | 1600 | 40 000 |
Разом | 150 | — | 5125 | 3725 | 176 875 |
Всього по господарству | 250 | — | 7300 | 5234 | 224 600 |
Розрахуємо спочатку середню врожайність по господарству:
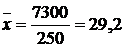 .
.
Далі визначаємо:
Для підрозділу № 1: 1) групову середню
2) середній квадрат варіантів ознаки
3) загальну дисперсію
| Для підрозділу № 2: 1) групову середню
2) середній квадрат варіантів ознаки
3) загальну дисперсію =1179,17-
|
Визначимо середню з групових дисперсій як середню арифметичну зважену із групових дисперсій:
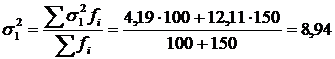 .
.
Знайдемо міжгрупову дисперсію:
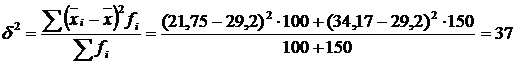 .
.
Тоді загальна дисперсія за урожайністю озимих зернових становитиме:
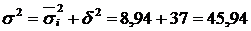 .
.
Отже, про зв'язок між досліджуваними ознаками можна судити за допомогою коефіцієнта детермінації, який є відношенням міжгрупової дисперсії до загальної і записується у вигляді формули
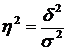 .
.
Коефіцієнт детермінації показує ступінь участі факторної ознаки у формуванні загальної змінюваності результативної ознаки. Зокрема, щодо нашого прикладу ступінь впливу кількості внесених добрив на урожайність зернових становить 80,5%:
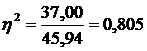 , або 80,5%.
, або 80,5%.
Ступінь впливу інших неврахованих факторів на результативну ознаку обчислюють за співвідношенням
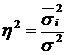
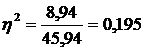 , або 19,5%.
, або 19,5%.
Рівень впливу інших неврахованих чинників дорівнює 19,5%.
Проте найчастіше в економічному аналізі в ролі показника тісноти зв'язку застосовується кореляційне відношення (емпіричне), яке є коренем другого ступеня із коефіцієнта детермінації. Формула його така:
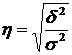 .
.
У нашому прикладі 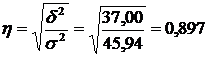 .
.
Це свідчить про те, що мінеральні добрива суттєво впливають на урожайність озимої пшениці.
Для підтвердження істотності зв'язку використаємо критерій Фішера
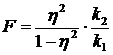 ,
,
де 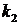 ,
, 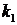 – число ступенів свободи;
– число ступенів свободи;
n – число одиниць сукупності;
m – кількість груп.
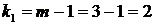 ;
; 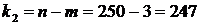 .
.
Отже, 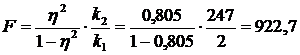 .
.
За допомогою таблиці критичних значень F-критерію порівняємо отриманий критерій із критичним значенням для рівня ймовірності 0,95. Для рівня значимості а = 0,05 табличне значення не перевищує 2,99. Оскільки розраховане значення критерію Фішера більше критичного (922,7 > 2,99), то це підтверджує істотність зв'язку між кількістю внесених добрив і урожайністю озимої пшениці.
12.2. Регресійний аналіз
12.3. Кореляційний аналіз
12.4. Кластерний аналіз
НАВЧАЛЬНИЙ ТРЕНІНГ
Розділ 13. МЕТОДИ ОПТИМІЗАЦІЇ ПОКАЗНИКІВ
13.1. Метод дерева рішень
13.2. Програмування
13.3. Аналіз чутливості
13.4. Метод Монте-Карло
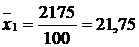 ;
;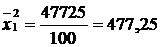 ;
;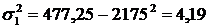 .
.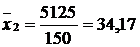 ;
;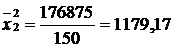 ;
;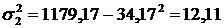 .
.