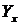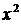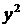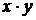Теорія економічного аналізу - Купалова Г.І. - 12.2. Регресійний аналіз

Під терміном "регресія" розуміють рух назад, повернення до попереднього стану. Названий термін ввів у кінці XIX ст. Френсіс Галтон. В результаті проведеного ним дослідження зв'язку між зростом батьків і дітей, виявилося, що наявна обернена залежність. Так, у батьків з дуже високим зростом діти мають менший зріст порівняно з середнім зростом батьків. І, навпаки, у дуже низьких батьків середній зріст дітей вищий. В одному і другому випадку середній зріст дітей прямує (повертається) до середнього зросту населення певної місцевості. Саме такою залежністю і пояснюють вибір терміна "регресія".

Регресійний аналіз (англ. regression analysis) – це метод визначення відокремленого і спільного впливу факторів на результативну ознаку та кількісної оцінки цього впливу шляхом використання відповідних критеріїв.

Регресійний аналіз проводиться на основі побудованого рівняння регресії і визначає внесок кожної незалежної змінної у варіацію досліджуваної (прогнозованої) залежної змінної величини.

Основним завданням регресійного аналізу є визначення впливу факторів на результативний показник (в абсолютних показниках). Передусім для цього необхідно підібрати та обґрунтувати рівняння зв'язку, що відповідає характеру аналітичної стохастичної залежності між досліджуваними ознаками. Рівняння регресії показує як в середньому змінюється результативна ознака (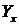) під впливом зміни факторних ознак (х_і).

У загальному вигляді рівняння регресії можна представити так:

,

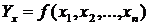де 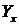– залежна змінна величина;

х – незалежні змінні величини (фактори).

Залежно від кількості змінних величин виділяють різні види регресійного аналізу. Якщо змінна величина завжди

одна, то змінних може бути як одна, так і декілька. Виходячи з цього, виділяють два види регресійного аналізу: парний (простий ) регресійний аналіз і регресійний аналіз на основі множинної регресії, або багатофакторний.

Парний регресійний аналіз – вид регресійного аналізу, що включає у себе розгляд однієї незалежної змінної величини, а багатофакторний – відповідно дві величини і більше.

Зважаючи на характер зв'язку, в регресійному аналізі можуть використовуватися лінійні та нелінійні функції. Для визначення характеру залежності та, відповідно, побудови рівняння регресії доцільно застосувати графічний метод, порівняння рівнобіжних рядів вихідних даних, табличний метод.

Так, графічний метод дає найбільш наочну картину розміщення крапок на графіку, завдяки чому можна виявити напрям і вид залежності між досліджуваними показниками: прямолінійна чи криволінійна.

За допомогою порівняння рівнобіжних рядів ознак можна спостерігати за рівномірністю їх взаємних змін. Якщо зміна факторної ознаки (х) призводить до відносно рівномірної зміни результативної (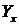), тоді використовується лінійна функція (наприклад, залежність між урожайністю культур і кількістю внесених добрив).

Найпростішим рівнянням парної регресії, що описує лінійну залежність між факторною і результативною ознаками, є рівняння прямої, яке має такий вигляд:

,

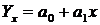де 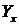– залежна змінна, яка оцінюється або прогнозується (результативна ознака);

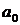– вільний член рівняння;

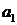– коефіцієнт регресії;

х – незалежна змінна (факторна ознака), яка використовується для визначення залежної змінної.

Параметри рівняння обчислюються на основі системи нормальних рівнянь методом найменших квадратів:

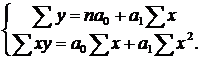
Звідси

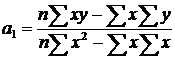
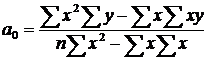, або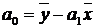

Для зручності розрахунків регресійного та кореляційного аналізу (розглянемо далі) доцільно використати таку форму таблиці (табл. 12.2).

Таблиця 12.2. Вихідні та розрахункові дані для обчислення регресійно-кореляційних характеристик (парна прямолінійна кореляція)

Основне змістовне навантаження в рівнянні регресії несе коефіцієнт регресії. Найчастіше застосовуються лінійні рівняння або приведені до лінійного вигляду. Коефіцієнт регресії – це кутовий коефіцієнт у прямолінійному рівнянні кореляційного зв'язку. У лінійній функції рівняння регресії він показує на скільки одиниць в середньому зміниться результативна ознака (у) при зміні факторної ознаки (х) на одиницю свого натурального виміру. Тобто, коефіцієнт регресії – це варіація у, яка припадає на одиницю варіації х. Коефіцієнт регресії має одиницю виміру результативної ознаки. За наявності прямого зв'язку коефіцієнт регресії є додатною величиною, а за зворотного зв'язку – від'ємною.

Параметр а₀ – вільний член рівняння регресії, тобто це значення у при х=0. Цей показник має тільки розрахункове значення у випадках, коли х не має нульових значень.

У разі, коли зі зміною факторної ознаки результативна змінюється нерівномірно, використовуються нелінійні функції. Так, якщо зміна факторного показника сприяла прискореній динаміці результативного показника (наприклад, вплив обсягу грошової маси на рівень інфляції), доцільно використати степеневу функцію:

.

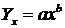У випадку, коли під впливом факторної ознаки результативна змінюється нерівномірно, причому з уповільненням, використовується рівняння гіперболи:

.

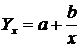Прикладом такої залежності є залежність рівня продуктивності праці робітників від рівня їх заробітної плати.

Якщо зміна факторної ознаки супроводжується нерівномірною варіацією факторної ознаки із зміною напряму зв'язку, нелінійна регресія описується рівнянням параболи:

.

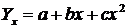Так, за допомогою функції параболи можна виразити залежність урожайності культур від кількості опадів.

Приклад. За даними 25 заводів дослідити залежність між рівнями озброєності праці основними засобами та її продуктивністю, використовуючи регресійний аналіз (табл. 12.3).

Таблиця 12.3. Озброєність праці основними засобами та рівень її продуктивності в групі заводів України, тис. грн

Паралельне зіставлення рядів значень рівнів озброєності праці основними засобами та її продуктивності, а також крапковий графік "кореляційного поля" (рис. 12.1) свідчать про наявність і напрям зв'язку (прямий) між наведеними показниками. Причому зміна озброєності праці (факторної ознаки х) приводить до відносно рівномірної зміни продуктивності праці (результативної ознаки у), що видно із графіка.

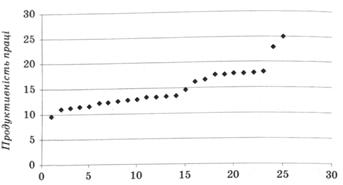
Рис. 12.1. Крапковий графік рівнів озброєності праці основними засобами та її продуктивності по 25 заводах України, тис. грн

Отже, можна зробити висновок про наявність між зазначеними ознаками парного прямолінійного зв'язку, який виражається найпростішим рівнянням регресії лінійної функції

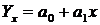
де 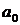– вільний член рівняння регресії;

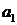– коефіцієнт регресії.

Для зручності розрахунків скористаємося наведеними нижче формулами, в які підставляємо попередньо обчислені необхідні розрахункові дані (табл. 12.1):

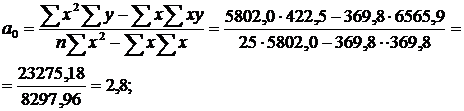
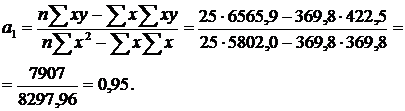
Рівняння залежності матиме такий вигляд:

.

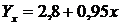Перевірка: 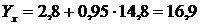, що відповідає середньому рівню продуктивності праці (табл. 12.3).

Зобразимо графічно залежність між рівнями озброєності праці основними засобами та її продуктивністю, використавши рівняння регресії (рис. 12.2).

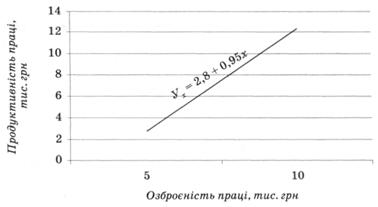
Рис. 12.2. Залежність між рівнями озброєності та продуктивності праці

Якщо підставити в отримане рівняння регресії відповідні значення фактора (х) по заводах, то одержимо вирівняні значення продуктивності праці залежно від озброєності її основними засобами. Результати розрахунків наведені в табл. 12.3 (остання графа).

З рівняння регресії видно, що підвищення озброєності праці основними засобами на одну тисячу гривень забезпечує підвищення рівня продуктивності праці на 0,95 тис. грн.

Якщо б на заводі під № 1 озброєність праці була вище середньої, наприклад 17,9 тис. грн, то виробіток продукції на одного працівника становив би 19,8 тис. грн:

.

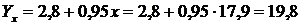Величина 17,9, яка взята на заводі, де озброєність праці перевищує середнє її значення – 14,8 тис. грн, називається середньою прогресивною.

Таким чином, регресійний аналіз може бути використаний ще й для визначення резервів шляхом застосування середньопрогресивного значення факторіальної ознаки. У наведеному прикладі цей резерв мають 19 заводів, що мають виробіток продукції на одного працівника менший за 19,8 тис. грн.

Також слід зазначити, що регресійний аналіз доцільно застосовувати для обґрунтування проектних, прогнозних чи очікуваних показників. Для цього необхідно підставити в одержане рівняння регресії проектне значення фактора. Зокрема, якщо б заводу № 7 поставити за мету доведення рівня озброєності праці основними засобами до 20 тис. грн, то можна зробити прогноз продуктивності праці, яка становитиме 21,8 тис. грн:

.

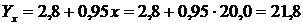Безумовно, що при застосуванні регресійного аналізу дотримуються деяких умовностей. Так, попередньо обумовлюється, що дія інших факторів, крім взятого за факторну ознаку, залишиться незмінною, а в дослідженні взято тільки один фактор.

Проте останню умовність можна усунути за допомогою застосування множинної регресії та кореляції, за яких підбирається значна кількість факторів.

Аналіз на основі множинної регресії (анг. multiple regression analysis) – вид регресійного аналізу, який ґрунтується на використанні в рівнянні регресії більше, ніж однієї незалежної змінної. Так, його застосовують при прогнозуванні попиту. Причому спочатку ідентифікуються фактори, що визначають попит, потім встановлюються наявні між ними взаємозв'язки та прогнозуються ймовірні майбутні їх значення. На основі отриманих даних виводиться прогнозне значення попиту.

Багатофакторне рівняння множинної регресії при лінійній залежності має такий вигляд:

,

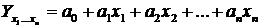де 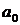– вільний член рівняння;

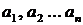– коефіцієнти регресії;

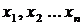– незалежні змінні (факторні ознаки);

n – кількість незалежних змінних.

Визначення параметрів множинної регресії вимагає трудомістких розрахунків із застосуванням комп'ютерних інформаційних систем. Однак одержані результати будуть достовірними і можуть широко використовуватися в економічній та управлінській діяльності насамперед для складання довгострокових прогнозів. Відомо, що однофакторна модель придатна для короткострокових прогнозів (на 2–3 роки).

Метод регресійного аналізу вважається найдосконалішим з усіх використовуваних нині нормативно-параметричних методів. Він широко застосовується для аналізу та встановлення рівня і співвідношень вартості продукції, яка характеризується наявністю одного або декількох техніко-економічних параметрів, що характеризують головні споживчі якості. Регресивний аналіз надає можливість знайти емпіричну форму залежності ціни від техніко-економічних параметрів товарів і виробів. При цьому він виступає в ролі цільової функції параметрів.

Метод регресійного аналізу особливо ефективний за умови здійснення розрахунків за допомогою сучасних інформаційних технологій і систем.