Інвестування - Гриньова В.М. - 3.1.2. Ризик портфеля інвестицій

Дотепер ризик і доходи розглядалися окремо за кожним активом. Однак компанії мають на своїх балансах різні активи й пасиви, а інвестори відповідно мають різні цінні папери у своїх портфелях. Очевидно, що гроші вкладені з метою одержання максимального доходу з найменшим ризиком. Однак важливо враховувати показники окремих активів з погляду співвідношення ризику й доходу, а також значний вплив цих співвідношень на ризикованість і прибутковість портфеля цінних паперів.

Визначення ризику й доходу всього портфеля починається з підрахунку стандартних відхилень і очікуваного доходу від окремих активів портфеля. Послідовність таких розрахунків було описано раніше. Завдання полягає в тому, щоб розподілити ризик на кілька активів чи цінних паперів або зменшити загальний ризик. Цього можна досягти двома способами: додатково вкласти гроші в різні цінні папери портфеля; знайти і придбати цінні папери, доходи від яких мають іншу амплітуду коливань, ніж ті, які вже є в портфелі.

Наповнення портфеля активами й цінними паперами до певної міри зменшує ризик. Однак, коли інвестори збільшують кількість цінних паперів з такими самими відхиленнями й коливаннями, як і ті, що вже є в портфелі, ризик не зменшиться. Ідея полягає в тому, щоб знайти цінні папери з різною амплітудою коливань.

Коваріація — це статистичний метод, що використовує для порівняння напрямків зміни двох змінних або, у цьому разі, активів у портфелі. Коефіцієнт кореляції, що змінюється від -1,0 до +1,0, встановлює межі, в яких доходи змінюються в одному напрямку.

Якщо при порівнянні характеристик одних активів, що входять до портфеля, з іншими визначений коефіцієнт кореляції (+1,0), то це вже означає, що напрямок руху доходів від цих активів однаковий. І, навпаки, при коефіцієнті кореляції (-1,0) зміни протилежні. Використовуючи метод коваріації для підрахунку коефіцієнтів кореляції різних активів портфеля, можна визначити і вибрати активи, які зводять ризикованість портфеля до мінімуму.

Сутність принципу коваріації подано на рис. 3.3.

Загальне правило таке: диверсифікованість (або вкладення в різні види цінних паперів) зменшує ризик. Чим більше в різних напрямках працюють різні активи портфеля, тим нижчий рівень ризику. Врахування цих особливостей портфеля інвестицій має вирішальне значення для затвердження рішень про інвестиції. Наприклад, деякі вкладники, які хочуть знизити ризик, можуть вирішити поповнити свої портфелі акціями або облігаціями, тому що ціни цих активів протягом усього циклу ділової активності змінюються в протилежному напрямку.

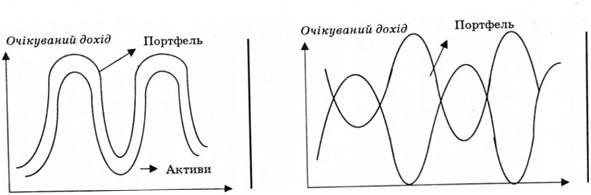
Рис. 3.3. Сутність принципу коваріації

Ризик однакових активів більший, ніж ризик портфеля активів у цілому. Чим більше в портфелі різних активів, тим більше розпорошується ризик. Це називається диверсифікованістю. Додавання нових активів до портфеля зменшує його нестабільність або ризик. Якщо коливання доходів від нових активів інші, ніж від доходів, які вже є в портфелі, загальний ризик портфеля знижується. Співвідношення коливань доходів від різних активів вимірюється у статистиці коваріацією. Коефіцієнт кореляції може змінюватися від +1,0 до —1,0. Нові активи з коефіцієнтом кореляції (+1,0) реагують так само, як і весь портфель інвестицій, і не зменшують ризик. Якщо коефіцієнт кореляції зменшується від +1,0 до —1,0, ризик портфеля також знижується.

Визначення ризику й віддачі портфеля може проводитися на основі моделі оцінки капітальних активів (МОКА) (Capital Asset Prissing Model — CAMP).

МОКА пов'язує прогнозований ризик з очікуваними доходами від проекту. її можна використати й для аналізу надійності і диверсифікованого ризику. Це стосується тісного зв'язку між доходами власників цінних паперів і загальних доходів ринку цінних паперів. Ці доходи, взяті окремо для акцій або для всього ринку, складаються з капітальних доходів і дивідендів.

Учені довели, що фондова біржа — високоефективний механізм, тому що вона швидко поєднує всю наявну інформацію. Якщо це так, то мінливість ринку дає загальний визначник для оцінки рівня ризику (або мінливості) індивідуальних активів і цінних паперів. Цей рівень ризику визначається чутливістю доходів від акцій до ситуації на ринку. Відповідно використовується інтерес (відсоток), що показує мінливість окремих акцій залежно від мінливості загального індексу, тобто ринку. Якщо доходи від певних акцій піднімаються або падають у відсотковому відношенні більше, ніж у цілому на ринку, то їх називають більш ризикованими, ніж ринок, і навпаки. Таким чином, ризикованість різних цінних паперів можна визначити простим порівнянням їхньої прибутковості із загальним індексом ринку.

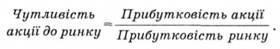
Наприклад, вкладник підрахував, що протягом 10 років середні річні доходи на ринку становили 5 %. Коли ж він підрахував результати за акціями, з'ясувалося, що прибутковість акції "А" в середньому становить 10 %, акції "Б" — 5 %, акції "В" — 3 %. Використовуючи загальний індекс, порівняйте прибутковість цих акцій з ринковою й визначте показники ризикованості кожного виду акцій.

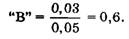
Тобто акції "А" більш чутливі, ніж ринок, акції "Б" мають ринкову чутливість, акції "В" – менш чутливі, ніж ринок.

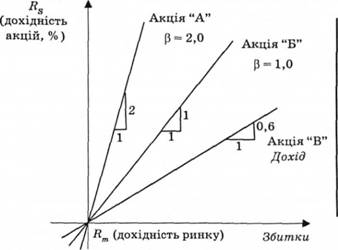
Рис. 3.4. β-коефіцієнт, який характеризує чутливість акцій

Характерні прямі на рис. 3.4 показують залежність між доходами від акцій і доходами ринку. Нахилу кожної лінії відповідає коефіцієнт р. Саме р визначає чутливість (або ризикованість) акцій порівняно із загальною прибутковістю ринку JRm. Ця залежність характеризується рівнянням

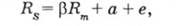
де а — константа;

е — величина помилки;

Р — коефіцієнт Р;

R_m — прибутковість ринку;

R_s — прибутковість акцій.

У моделі МОКА значення ай е прирівнюються до нуля. За такої умови прибутковість акцій (R) та їхні показники Р визначаються винятково їхньою залежністю від ринку (R_m). Коли залежність прибутковості акцій і ринку на графіку зображується прямою з кутом нахилу 45°, це означає пряму залежність, тобто 1:1. Інакше кажучи, зміна на 1 % прибутковості ринку змінює на 1 % прибутковість акцій. Акції, які мають ринкову прибутковість або ж мають однакову з ринком чутливість, будуть мати коефіцієнт р = 1,0.

Коли для аналізу використовують коефіцієнт Р, то зрозуміло, що вихідною точкою для порівняння ризику цінних паперів або активів повинен бути коефіцієнт Р = 1,0 або одинична дохідність. Доходи акції "Б", що має р = 1,0, будуть змінюватися однаково з ринком, тобто їхній ризик також не диверсифікований, як і весь ринок цінних паперів. Акції "В", де Р = 0,6, мають мінливість (нестійкість) менше ринкової, тобто менш ризикові, ніж ринок. Акції "А" з коефіцієнтом р = 2,0 більш ризикові, ніж ринок.

Природно, що МОКА дає змогу легко порівняти ризикованість окремих акцій. Однак важливою умовою є те, що дисперсія навколо характерної лінії не повинна бути великою. Якщо дисперсія більша, то варто враховувати додаткові елементи ризику, а ринок цінних паперів може й не бути точним показником ризикованості окремих цінних паперів.

На практиці використовують відомі ринкові показники (у тому числі й прибутковість ринку), такі як 500 індексів компанії "Стандарт і Пур", які добре відображають ринок.

Модель оцінки капітальних активів дає можливість порівняти і визначити залежність між прибутковістю окремих акцій і прибутковістю ринку цінних паперів. Ринок — це стандартний визначник не диверсифікованого ринку, що іноді називають "систематичним". Ступінь чутливості акцій до ринку називається "бета" (β). Якщо β = 1,0, то всі цінні папери з β > 1,0 більш ризиковані, ніж ринок; цінні папери з β < 1,0 менш ризиковані, ніж ринок. Створюючи портфель цінних паперів, вкладники, які обирають акції з низьким β, напевно будуть мати більш низькі доходи, ніж вкладники, які обирають акції з більш високим показником р (а отже, і більш ризиковані).

Як зазначалось, необхідна величина прибутковості активів складається з безпечної ставки та премії за ризик. Якщо використовується оцінка за допомогою р, то премія за ризик складається з ринкового доходу (R_m) + (-) вищий або нижчий не диверсифікований ризик, пов'язаний з певними акціями. Тепер маємо інструмент аналізу залежності ризику й доходу акцій у разі, коли ринок є стандартом виміру ризику. Інакше кажучи, за певного рівня ризику прибутковості ринку можна визначити необхідну величину прибутковості певних акцій. Усе, що треба зробити, — це підрахувати безпечну ставку, взяти середню ринкову ставку і скорегувати її з урахуванням ризикованості окремих акцій. Нехай безпечна ставка дорівнює б % (як обчислено раніше), а середня прибутковість ринку цінних паперів — 10 %, тоді як для акцій р = 1,2. Маючи такі дані, можна визначити необхідну величину прибутковості, яку відповідно до вимог ринку повинні мати окремі акції. Формула для визначення необхідної ставки доходу RRR така:

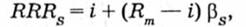
де RRRS — необхідна прибутковість акцій;

і — безпечна ставка;

R — середня прибутковість ринку;

β — не диверсифікований ризик.

Тоді: RRRs = 0,05 + (0,1 — 0,05)·1,2 = 0,11, або 11 %.

Величина 11 % означає, що будь-які акції з ризиком, або Р s 1,2, повинні давати дохід не менший ніж 11 %. Дохід, нижчий ніж 11 %, робить акції непривабливими; їх варто продати. Дохід, вищий ніж 11 %, означає, що на акції занижена ціна, їх варто купувати. Цю взаємозалежність показано на рис. 3.5 лінією надійності ринку (ЛНР) (Security market line — SML), що є графічним зображенням МОКА.

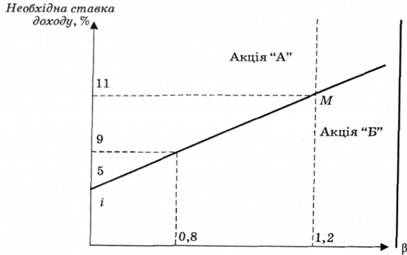
Рис. 3.5. Лівія надійності ринку: М — прибутковість ринку; і — безпечна ставка

Необхідно звернути увагу на те, що різні необхідні величини прибутковості акції можна визначити, коли відомі ЛНР і коефіцієнти р різних акцій. Акції з β = 0,8 будуть мати RRRs = 9 %, а акції з β = 1,2 будуть мати необхідну ставку доходу 11 %. ЛНР дає базис для оцінки відносних переваг цінних паперів.

Наприклад, акції "Б" можуть принести дохід 13 %, тоді як ЛНР показує, що досить мати 11 %. Ціна цих акцій занижена, і їх треба купувати. У випадку з акціями "А" за β = 1,2 вони повинні давати 11 % доходу, а дають нижчий дохід, тобто акції ИА" треба продавати, вони не вигідні (нижче ЛНР). Якщо ціль — мати низький ризик, то в портфель інвестицій варто внести акції з низьким p. І навпаки, якщо мета — отримати більше доходів, то інвестори повинні поповнити портфель акціями з високими р.

Безумовною перевагою застосування МОКА й ЛНР є простота. МОКА — це дуже корисний інструмент для оцінки цінних паперів, тому що він визначає необхідну ставку доходу (дисконтну ставку), яку можна використати для визначення теперішньої вартості цінних паперів. Замість того, щоб застосовувати формулу

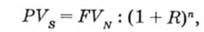
ті самі результати можна отримати за допомогою формули

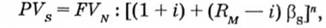
де PVs — сьогоднішня вартість очікуваних доходів;

FV_N — майбутня вартість очікуваних доходів;

R — ставка дисконту або необхідна ставка доходу;

n — число періодів або років;

і — безпечна ставка;

R_m — середня прибутковість ринку;

βs — бета для окремих активів або акцій.

Модель Л HP починається з безпечної ставки, потім додається премія, що складається із середньої прибутковості ринку й виправлення коефіцієнта р, або диверсифікованого ризику. Метод ЛНР дає змогу визначити ставку доходу, який повинні одержувати інвестори від цінних паперів. Якщо прибутковість ціни паперів нижча, ніж ця ставка, то це означає, що інвестори одержують менше ніж треба, тобто ціна на цінні папери занадто висока. Якщо прибутковість вища, ніж необхідна ставка, то інвестори одержують більше, ніж повинні одержувати, а це означає, що гроші вкладені вигідно. Крім того, обчислюючи дисконтну ставку, метод ЛНР допомагає інвесторам визначити теперішню вартість і прибутковість інвестицій.

Обидва методи (для визначення ризику за стандартним відхиленням або за показником р) дають базу для оцінки цінних паперів та інших активів. МОКА і ЛНР не безпомилкові. Можуть бути інші, більш важливі фактори, крім ринку, які впливають на прибутковість цінних паперів. У цьому випадку р не буде надійним показником не диверсифікованого ризику. Подібна ситуація з використанням статистичних рядів за певний період часу — це не найкращий спосіб для визначення очікуваних доходів. Однак, хоча МОКА й ЛНР дають лише приблизні значення, вони є важливим інструментом визначення взаємозалежності ризику й доходу, а також вартості акцій.