Моделі і методи прийняття рішень в аналізі та аудиті - Гаркуша Н.М. - 8.3.2. Метод внутрішньої норми прибутку

Внутрішня норма прибутку (ВНП, інші назви - внутрішня норма прибутковості, внутрішня норма дисконту, внутрішня норма рентабельності, international rate of return (IRR)) є показником, що широко використовується під час аналізу ефективності інвестиційних проектів.

Реалізація будь-якого інвестиційного проекту вимагає залучення фінансових ресурсів, за які завжди необхідно платити. Так, за позикові засоби платять відсотки, за залучений акціонерний капітал дивіденди і т. ін.

Показник, що характеризує відносний рівень цих витрат, є ціною за використаний (що авансується) капітал. При фінансуванні проекту з різних джерел цей показник визначається за формулою середньої арифметичної зваженої.

Щоб забезпечити дохід від інвестованих засобів або принаймні їх окупність, необхідно досягти такого становища, коли чиста поточна вартість буде більше нуля або дорівнюватиме йому.

Для цього потрібно підібрати таку відсоткову ставку для дисконтування членів потоку платежів, яка забезпечить отримання виразів NPV > 0 або NPV = 0.

Така ставка (бар'єрний коефіцієнт) має відображати очікуваний усереднений рівень позикового відсотка на фінансовому ринку з урахуванням чинника ризику.

Тому під внутрішньою нормою прибутку розуміють ставку дисконтування, використання якої забезпечує рівність поточної вартості очікуваних грошових відпливів і поточної вартості очікуваних грошових припливів, тобто при нарахуванні на суму інвестицій відсотків за ставкою, рівною внутрішній нормі прибутку, забезпечується отримання розподіленого в часі доходу.

Показник внутрішньої норми прибутку (IRR) характеризує максимально допустимий відносний рівень витрат, які можуть бути здійснені під час реалізації проекту.

Наприклад, якщо для реалізації проекту була отримана банківська позика, то значення IRR показує верхню межу допустимого рівня банківської відсоткової ставки, перевищення якої робить проект збитковим.

Таким чином, значення цього показника полягає в тому, що інвестор повинен порівняти отримане для інвестиційного проекту значення IRR із ціною залучених фінансових ресурсів (cost of capital - СС):

o якщо IRR > СС, то проект слід прийняти;

o якщо IRR < СС - проект слід відкинути;

o якщо IRR -СС - проект ні прибутковий, ні збитковий. Для розрахунку внутрішньої норми прибутку можна використовувати таке рівняння:

де ЧД, - чистий грошовий дохід і-го року, грн;

п - кількість періодів експлуатації проекту, років;

Р0 - первинні вкладення на реалізацію інвестиційного проекту, грн;

IRR - внутрішня норма прибутку.

Розрахуємо значення внутрішньої норми прибутку (IRR) за даними таких прикладів:

А. У разі, коли передбачувані грошові надходження очікуються в кінці терміну реалізації інвестиційного проекту.

Приклад 8.5

Підприємство інвестувало 10 000 грн і має намір у кінці четвертого року реалізації інвестиційного проекту отримати 18 106 грн грошового доходу. Необхідно визначити, яка внутрішня норма прибутку необхідна для того, щоб дисконтований грошовий дохід четвертого року дорівнював вартості інвестиційного проекту.

Для цього складемо рівняння:

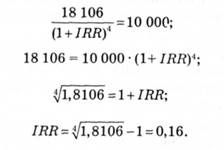
Таким чином, внутрішня норма прибутку буде дорівнювати 0,16, або 16%.

Б. Уразі рівномірних грошових надходжень (ануїтету ).

Слід зазначити, що у фінансових розрахунках ануїтет є рівними по величині грошовими потоками за кожний період протягом точно визначеного часу.

Приклад 8.6

На купівлю машини потрібно 16 950 ум. од. Машина протягом 10 років економитиме щорічно 3000 ум. од. Залишкова вартість машини рівна нулю. Необхідно знайти IRR,

Знайдемо відношення необхідного значення інвестиції до щорічного припливу грошей, яке збігатиметься з множником якого-небудь (поки невідомого) коефіцієнта дисконтування:

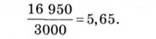
Отримане значення фігурує у формулі визначення сучасного значення ануїтету:

За допомогою фінансової таблиці коефіцієнтів приведення ануїтетів (додаток В) знаходимо, що для п = 10 і значенні коефіцієнта ануїтету, що дорівнює 5,65, показник дисконту становить 12 %. Перевіримо правильність розрахунків (табл. 8.4).

Таблиця 8.4. Перевірка правильності розрахунків

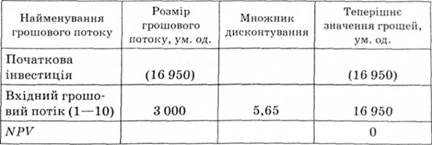
Таким чином, ми знайшли і підтвердили, що IRR =12 %. Успіх рішення був забезпечений збігом відношення початкової суми інвестицій до величини грошового потоку з конкретним значенням множника дисконту з фінансової таблиці. В. Уразі нерівномірних грошових надходжень. Практичне застосування цього методу ускладнене, якщо у розпорядженні аналітика немає спеціалізованого фінансового калькулятора. У цьому випадку застосовується метод послідовних ітерацій із використанням табульованих значень дисконтованих множників. Для цього за допомогою таблиць вибираються два значення коефіцієнта дисконтування rt < г2 так, щоб в інтервалі (г , гЛ функція NPV змінювала своє значення з " + " на "-" або з на " + Далі застосовують формулу

де гх - значення табульованого коефіцієнта дисконтування, при якому NPV > 0 (< 0);

гг - значення табульованого коефіцієнта дисконтування, при якому NPV< 0 (> 0).

Точність обчислень обернено пропорційна довжині інтервалу (rv г2), а найкраща апроксимація з використанням табульованих значень досягається у разі, коли довжина інтервалу мінімальна (рівна 1 %), тобто г} і г2 найближчі один до одного значення коефіцієнта дисконтування, що задовольняють умови (у разі зміни знака функції з " + " на "-"):

гх - значення табульованого коефіцієнта дисконтування, що мінімізує позитивне значення показника NPV;

г2 - значення табульованого коефіцієнта дисконтування, що максимізує негативне значення показника NPV.

Шляхом взаємної заміни коефіцієнтів гх і г2 аналогічні умови виписуються для ситуації, коли функція міняє знак із на " +

Приклад 8.7

Необхідно визначити значення показника IRR для проекту, розрахованого на три роки, що вимагає інвестицій у розмірі 20 тис. грн і має передбачувані грошові надходження у розмірі 6 тис. грн, 4 тис. грн, 14 тис. грн.

Візьмемо два довільні значення коефіцієнта дисконтування: /*, = 15 %, г2 - 20 %, Відповідні розрахунки з використанням табульованих значень наведені в табл. 8.5 і 8.6.

За даними розрахунків І і II обчислимо значення IRR:

Уточнимо величину ставки, для чого приймемо значення відсоткових ставок при г - 16 %; при г -17 %. Проведемо новий розрахунок;

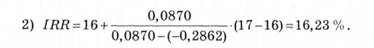
IRR= 16,23 % є верхньою межею відсоткової ставки, за якою підприємство може окупити кредит для фінансування інвестиційного проекту. Для отримання прибутку підприємство має брати кредит за ставкою менше 16,23 %. Зазначимо, що з практичного погляду така точність є зайвою.