Фінанси регіону - Коваленко М.А. - 3.2. Прогнозування фінансового стану регіону

При обґрунтуванні й виборі управлінських рішень, пов'язаних із забезпеченням фінансового розвитку регіону, важливу роль відіграють методи прогнозування, що дозволяють знаходити найбільш ефективні шляхи розвитку регіону на основі всебічного ретроспективного аналізу і вивчення тенденцій його розвитку [12].

У загальному випадку прогнозування в управлінні безпечним фінансовим розвитком регіону дозволяє:

^ визначити можливі цілі та напрями фінансування розвитку регіону;

^ оцінювати соціально-економічні наслідки реалізації кожного з можливих варіантів розвитку регіону;

^ визначити перелік заходів, необхідних для забезпечення кожного з можливих варіантів розвитку регіону;

* оцінювати обсяг ресурсів, необхідних для здійснення намічених програм розвитку регіону.

Розроблення прогнозів стану фінансової системи регіону здійснюється відповідно до основних методологічних принципів прогнозування [12,8,31].

Принцип системності вимагає взаємозв'язаності та співпідпорядкованості прогнозів об'єкта прогнозування і прогнозного фону, під яким розуміється сукупність зовнішніх стосовно до об'єкта умов, істотних для розв'язання завдання прогнозу. Щодо прогнозування розвитку регіону цей принцип означає врахування впливу на стан фінансової безпеки регіону як внутрішніх, так і зовнішніх загроз фінансовій безпеці, виражених значеннями показників фінансової безпеки регіону.

Принцип динамічності забезпечує перехід від статичного аналізу показників фінансової безпеки регіону до динамічного, що припускає зміни значень показників і зв'язків між ними в часі.

Принцип безперервності потребує безупинного коректування й уточнення прогнозів, оскільки результати прогнозу дійсні тільки протягом обмеженого періоду часу. Принцип припускає визначення оптимальної величини циклу прогнозування.

Принцип багатоваріантності. Імовірнісний характер прогнозу вимагає розроблення альтернативних варіантів розвитку стану фінансової безпеки регіону за декількома напрямами з наступним вибором оптимального варіанта.

Принцип комплексності (погодженості) допускає використання в діалектичній єдності двох методичних підходів; дослідницького (пошукового) й нормативного (цільового). Принцип уможливлює узгодження пошукових І нормативних прогнозів різної природи та різного періоду попередження.

Принцип верифікованості вимагає визначення вірогідності, точності й обґрунтованості прогнозів.

Принцип об'єктивності потребує високого ступеня відповідності прогнозованого і здійсненого (реального) стану регіону. Ступінь об'єктивності прогнозу визначається такими факторами: якістю й вірогідністю вихідної інформації, адекватністю використовуваних методів прогнозування, термінами прогнозування. Принцип допускає вибір та обґрунтування критеріїв якості прогнозу.

Принцип конкретності вимагає високого ступеня вірогідності вихідних даних, використовуваних для одержання прогнозу.

При прогнозуванні фінансового розвитку регіону пропонується використовувати фактографічні статистичні методи. Під фактографічними розуміються методи прогнозування, що базуються на фактично наявному інформаційному матеріалі про стан фінансової системи регіону, на відміну від експертних методів, які ґрунтуються на інформації, одержуваній від фахівців-експертів. Статистичними є методи, які здійснюють обробку вихідної кількісної інформації за принципом виявлення математичних закономірностей, що містяться в ній, і взаємозв'язків між вихідними показниками.

Із сукупності виділених статистичних методів прогнозування пропонується використовувати такі методи прогнозування, як виявлення тренду. Суть цього методу полягає в тому, що за графіком наявних ретроспективних значень аналізованого часового ряду візуально визначають форму моделі, .яка описує його поведінку. У випадку, якщо отримана модель задовольняє низку критеріїв, вона визнається такою, що адекватно описує досліджуваний процес чи явище і використовується для прогнозування. При цьому усі відхилення вихідних спостережень від одержаної залежності вважаються випадковими. Вдосконалені методики виявлення тренду, крім візуального аналізу, використовують такі операції, як згладжування часового ряду, що дозволяє візуалізувати тренд; присвоєння ретроспективним спостереженням часового ряду спадних ваг, які дозволяють одержати більш точний прогноз та ін.

Наступним етапом побудови моделі управління фінансовим розвитком регіону є побудова комплексу часових моделей аналізу показників фінансового розвитку. Основна мета - на їх основі зробити прогноз про розвиток досліджуваного процесу на певний період.

Існує досить велика кількість моделей аналізу рядів динаміки, однак для досягнення цілей часто використовуються моделі декомпозиції. їм притаманні наступні переваги:

^ дані моделі дозволяють проаналізувати у взаємозв'язку основну тенденцію розвитку (тренд) і циклічну складову процесу, що стосовно цього дослідження дозволяє визначити фази розвитку кризи в різних сферах економіки;

^ моделі декомпозиції досить адекватно відображають процеси, які проходять у часі.

Моделі декомпозиції містять у собі чотири складові:

1) тренд (Т) - основну тенденцію розвитку процесу;

2) циклічну складову (С), що характеризує циклічні коливання в економіці;

3) сезонну складову (S), що характеризує сезонність економічних явищ;

4) випадкову складову (І), що відображає вплив випадкових факторів.

Оскільки моделі декомпозиції представляють розподіл (декомпозицію) вихідного ряду, то для подальшого прогнозування необхідно провести синтез цих складових. Композиція виконується за допомогою операторів додавання і множення, в зв'язку з тим виділяються два основних види моделей декомпозиції [76]: адитивні моделі, які мають наступний загальний вигляд:

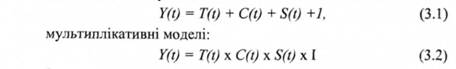
Застосування адитивних і мультиплікативних моделей зумовлено різницею у розвитку економічних процесів. Адитивні моделі

доцільно застосовувати за умови незначної мінливості амплітуди коливань економічного процесу, мультиплікативні моделі застосовуються при зростаючій амплітуді коливань.

Необхідно зазначити, що сезонна складова також є циклічною складовою з певним періодом, тому для більш якісного аналізу циклічності економічних змін у різних сферах економіки доцільно розглядати сезонну складову як елемент циклічної.

Під трендом розуміють зміни, котрі визначають загальне направлення розвитку, основну тенденцію часових рядів. У зв'язку з цим економіко-математична динамічна модель, у якій розвиток модельованої економічної системи відображається через тренд її основних показників, називається трендовою моделлю. Для виявлення тренда в часових рядах, а також для аналізу трендових моделей використовується апарат теорії ймовірності та математичної статистики, розроблений для простих статистичних сукупностей.

Попередній аналіз часових рядів економічних показників полягає, як правило, у виявленні й усуненні аномальних значень рівнів ряду, а також у визначенні наявності тренду у вихідному часовому ряді.

Для визначення наявності тренду у вихідному часовому ряді використовується декілька методів. Можливо застосувати метод Фостера-Стюарта, який має великі можливості та дає більш надійні результати порівняно з іншими методами [76, с. 138]. Крім тренду самого ряду, він дозволяє встановити наявність тренду дисперсії часового ряду: якщо тренду дисперсії немає, то розкид рівнів ряду постійний; якщо дисперсія збільшується, то ряд "розкачується" тощо.

Реалізація методу складається з чотирьох етапів.

На першому етапі проводиться порівняння кожного рівня вихідного часового ряду, починаючи з наступного рівня, зі всіма попередніми, при цьому визначаються дві числові послідовності:

На третьому етапі перевіряються гіпотези:

1) чи можна вважати випадковими відхилення величини s від величини μ - математичного очікування величини s для ряду, в якому рівні розміщені випадково;

2) чи можна вважати випадковими відхилення величини d від нуля.

Ця перевірка проводиться з використанням розрахункових значень t- критерію Стьюдента для середньої та дисперсії:

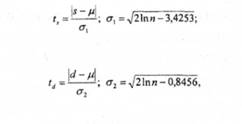
На четвертому етапі розраховані значення ts i td порівнюються з табличними значеннями t- критерію Стьюдента із заданим рівнем значимості t_а. Якщо розраховане значення менше від табличного, то гіпотеза про відсутність відповідного тренду приймається; в іншому випадку тренд є. Якщо більше від табличного значення ї _ф а и менше від ї а, то для цього часового ряду є тренд у середньому, а тренду дисперсії рівня ряду немає.

Дуже часто рівні економічних рядів динаміки коливаються, при цьому тенденція розвитку економічного явища в часі приховується випадковими відхиленнями рівнів у ту або іншу сторону. З метою більш чітко виявлення тенденції розвитку досліджуваного процесу, в тому числі для подальшого застосування методів прогнозування на основі трендових моделей, роблять згладжування (вирівнювання) часових рядів.

Серед методів вирівнювання часових рядів існує метод експоненційного згладжування. Його особливість полягає в тому, що в процедурі перебування згладженого рівня використовуються тільки попередні рівні ряду, взяті з визначеною вагою, причому вага спостереження зменшується в міру видалення його від моменту часу, для якого визначається згладжене значення рівня ряду. Якщо для вихідного часового ряду у_ь у₂, уз, у_n відповідні згладжені значення рівнів позначити через St де t = 1,2...,n, то експонентне згладжування здійснюється за формулою

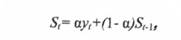
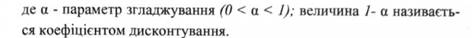
Використовуючи наведене вище рекурентне співвідношення для всіх рівнів ряду, починаючи з першого і закінчуючи моментом часу t, можна отримати, що експонентна середня, тобто згладжене цим методом значення рівня ряду, є зваженою середньої всіх попередніх рівнів:

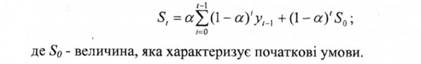
У практичних задачах обробки економічних часових рядів рекомендується вибирати величину параметра згладжування в інтервалі від 1,3 до 0,3. Інших точних рекомендацій для вибору оптимальної величини параметра поки що немає. В окремих випадках Р. Браун пропонує визначати величину а, виходячи з довжини ряду, який згладжуємо:

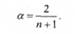
Що стосується початкового параметра Sо, то в конкретних задачах його беруть або рівним значенню першого рівня ряду у₁, або рівним середній арифметичній декількох перших членів ряду, наприклад, членів y1,y2, y3:

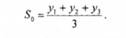
Зазначений вище порядок вибору величини Бо забезпечує добре узгодження згладженого і вихідного рядів для перших рівнів. Якщо при проході до правого кінця часового ряду згладжені цим методом значення при вибраному параметрі починають значно відрізнятися від відповідних значень вихідного ряду, необхідно перейти на інший параметр згладжування. Слід відмітити, що при цьому методі згладжування не губляться ні початкові, ні кінцеві рівні часового ряду, які згладжуємо.

Аналізуючи часові ряди показників фінансового розвитку регіону можливо прийти до висновку, що відсутній тренд у показника "індекси споживчих цін" через те, що його значення є відношенням, яке завжди близьке до 100 %. Тренди інших показників фінансового розвитку будуються за річними даними. Інформаційною базою значень показників служать дані з офіційних джерел Головного управління статистики у регіоні та Департаменту інформаційних технологій МВС України [71,79,80]. Результати здійснених розрахунків відображені в таблиці 3.2. Для прикладу розрахунки проведено [76] на матеріалах Харківської області.

Таблиця 3.2. Тренди основних показників фінансової безпеки Харківської області на 2007-2008 рр.

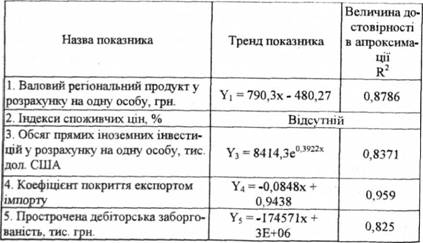
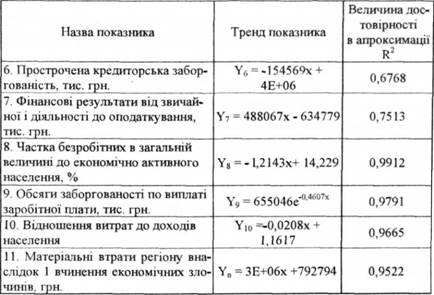
При побудові тренду деяких показників вилучались так звані "випадкові" значення, які замінювалися середнім сусідніх значень. Такі випадкові значення значно відхиляються від динаміки часового ряду і ускладнюють прогнозування значень показника Наявність випадкових значень показників пояснюється впливом на них тимчасових суспільних процесів. Так, при побудові тренду "прострочена дебіторська заборгованість" було виключено значення 2005 року, "прострочена кредиторська заборгованість" - значення 2004 року, "фінансові результати від звичайної діяльності до оподаткування" - значення 2003 року (від'ємне значення). При побудові тренду "обсягу прямих іноземних інвестицій" за кожний рік було виявлено значне вилучення інвестицій у 2002 році. Це значення показника також було вилучено.

Побудова трендів показників фінансової безпеки Харківської області здійснювалась через лінійну функцію, що в подальшому полегшувало процес прогнозування його значень. Тренд "обсяг прямих іноземних інвестицій" та "обсяги заборгованості з виплати заробітної плати" описані експоненціальною функцією.

Інтерпретація параметрів рівнянь трендів описує динамікою показників фінансової безпеки Харківської області: число а характеризує початковий рівень часового ряду в момент часу t = 0, число b - це середній за одиницю часу (в цьому випадку за рік) коефіцієнт зростання значень показника.

Таким чином, було розроблено трендові моделі для досліджуваних значень показників фінансового стану Харківської області. Тренди свідчать про позитивну їх динаміку, крім показників "матеріальні втрати внаслідок здійснення економічних злочинів" та "коефіцієнта покриття експортом імпорту", значення яких погіршуються для стану фінансової системи регіону.

Прогнозування економічних показників на основі трендових моделей, к і більшість інших методів економічного прогнозування, ґрунтується на ідеї екстраполяції. Під екстраполяцією розуміється поширення закономірностей, зв'язків і співвідношень, що діють у досліджуваному періоді за його межами. У більш широкому змісті слова її розглядають як отримання уявлення про майбутнє на основі інформації, що відноситься до минулого і сьогодення. У процесі побудови прогнозних моделей у їх структуру іноді закладаються елементи майбутнього передбачуваного стану об'єкта або явища, але в цілому ці моделі відбивають закономірності, що спостерігаються в минулому й сьогоденні, тому достовірний прогноз можливий лише щодо таких об'єктів та явищ, які значною мірою детермінуються минулим і сьогоденням.

Існують дві основні форми детермінації: внутрішня і зовнішня. Внутрішня детермінація, або само детермінація, більш стійка, її простіше ідентифікувати з використанням математичних моделей. Зовнішня детермінація визначається великим числом факторів, усі їх урахувати практично неможливо. Якщо деякі методи моделювання, наприклад адаптивні, відображають загальний сукупний вплив на економічну систему зовнішніх факторів, тобто відображають зовнішню детермінацію, то методи, які базуються на використанні трендових моделей економічних процесів, представлених одномірними часовими рядами, відображають внутрішню детермінацію об'єктів і явищ.

При екстраполяційному прогнозуванні економічної динаміки на основі часових рядів із використанням трендових моделей виконуються наступні основні етапи:

1) попередній аналіз даних;

2) формування набору моделей (наприклад, набору кривих зростання), так званими функціями-кандидатами;

3) чисельне оцінювання параметрів моделей;

4) визначення адекватності моделей;

5) оцінка точності адекватних моделей;

6) вибір кращої моделі;

7) одержання точкового й інтервального прогнозів;

8) верифікація прогнозу.

Порядок реалізації перших шести етапів розглянуто вище. Розглянемо більш докладно два завершальних етапи.

Прогноз на підставі трендових моделей (кривих зростання) містить два елементи: точковий та інтервальний прогнози. Точковий прогноз - це прогноз, яким називають єдине значення прогнозованого показника. Це значення визначається підстановкою в рівняння вибраної кривої росту величини часу t, що відповідає періодові попередження: t = n + 1;t = n + 2 і т. д. Такий прогноз називається точковим, тому що на графіку його можна відобразити у вигляді точок.

Очевидно, що точний збіг фактичних даних у майбутньому і прогностичних точкових оцінках малоймовірний. Тому точковий прогноз повинен супроводжуватися двосторонніми межами, тобто вказівкою інтервалу значень, у якому з достатньою долею впевненості можна очікувати появи прогнозованої величини. Встановлення такого інтервалу називають інтервальним прогнозом.

Інтервальний прогноз на базі трендових моделей здійснюється шляхом розрахунку довірчого інтервалу - такого інтервалу, в якому з визначеною ймовірністю можна очікувати появи фактичного значення прогнозованого економічного показника. Розрахунок довірчих інтервалів при прогнозуванні з використанням кривої росту спирається на висновки і формули теорії регресій. Перенесення висновків теорії регресій на часові економічні ряди не зовсім правомірне, оскільки динамічні ряди відрізняються від статистичних сукупностей. Тому до оцінювання довірчих інтервалів для кривих росту варто підходити з обережністю.

Методи, розроблені для статистичних сукупностей, дозволяють визначити довірчий інтервал, що залежить від стандартної помилки оцінки прогнозованого показника, від часу попередження прогнозу, від кількості рівнів у часовому ряді й від рівня значимості (помилки) прогнозу.

У випадку прямолінійного тренду для розрахунку довірчого інтервалу можна використовувати аналогічну формулу для парної регресії. Таким чином довірчий інтервал можна використовувати для прогнозу U в цьому випадку буде мати вигляд

Таким чином, формули розрахунку довірчого інтервалу для трендових моделей відбивають динамічний аспект прогнозування, тобто збільшення невизначеності прогнозованого процесу зі зростанням періоду попередження виявляється в постійному розширенні довірчого інтервалу.

Незважаючи на громіздкість деяких формул, розрахунок точкових й інтервальних прогнозів на основі трендових моделей у формі кривої росту технічно є досить простою процедурою. Однак не слід захоплюватися технічною простотою процедури екстраполяції і намагатися заглянути занадто далеко, це неминуче приведе до грубих помилок. Оптимальна довжина періоду попередження визначається окремо для кожного економічного явища. Ця довжина, як правило, не перевищує для рядів річних спостережень однієї третини обсягу даних, а для квартальних та місячних рядів - двох років.

У результаті здійснення прогнозу значень показників фінансового стану регіону [76] отримав наступні їх значення, відображені в таблиці 3.3. Побудовано економетричні моделі прогнозування показників фінансового стану Харківської області та дано прогноз значень цих показників станом на 2007-2008 роки.

Таблиця 3.3. Прогноз основних показників фінансової безпеки Харківської області на 2007-2008 рр.

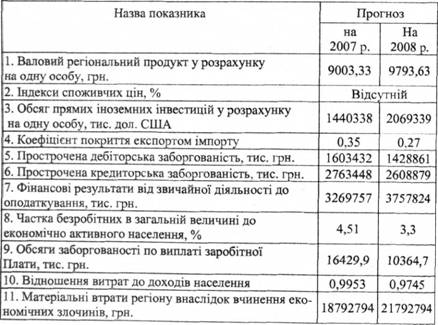
Для кращого аналізу часових рядів показників фінансової безпеки регіону необхідно розглядати в місячному або квартальному розрізі. Не завжди є така можливість: значення одних формуються за методологією Державної статистики лише в річному вираженні, по інших - не завжди вдається зібрати статистичні дані за бажаний період. Виходячи з цього, [76] здійснював відповідний аналіз значень таких показників фінансової безпеки Харківської області, як "індекси споживчих цін" та "відношення витрат до доходів населення".

Аналіз розпочато з показника відношення витрат до доходів населення. Попередній аналіз дозволив висунути припущення про наявність сезонних коливань показника "відношення витрат до доходів". Перевірку висунутої гіпотези можна зробити за допомогою розрахунку авто кореляційної функції (послідовності коефіцієнтів автокореляції), вираз якої має такий вигляд:

Із рис. 3.1 видно, що має місце квартальний ефект сезонності. Цей факт також наочно можна побачити на графіку (рис. 3.2).

Визначимо кількісні закономірності, пов'язані з ефектом сезонності для показника "відношення витрат до доходів населення". Використаємо наступну модель:

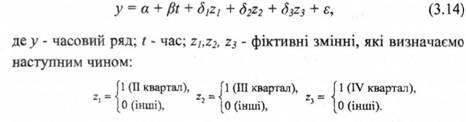
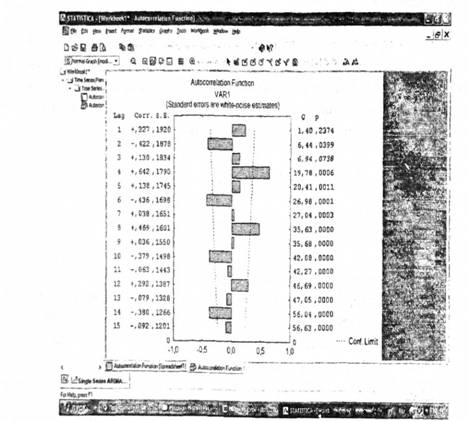
Рис. 3.1. Автокореляційна функція даних показника "відношення витрат

до доходів"

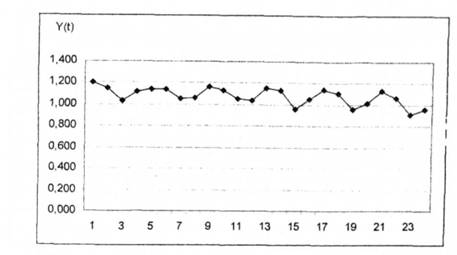
Рис. 3.2. Графік показника "відношення витрат до доходів населення"

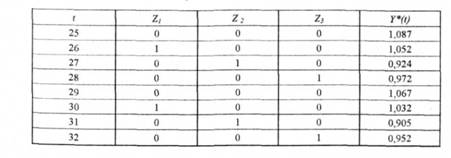
У моделі параметри α, βt, δ1, δ2, δ3- невідомі і їх слід оцінити, наприклад, методом найменших квадратів. Випадкова величина є відображає дію на,у всіх інших факторів.

Зауважимо, що подібний спосіб введення трьох фіктивних змінних передбачає визначення першого кварталу еталоном.

Початкові дані для оцінювання п'яти параметрів рівняння множинної регресії відображено в таблиці 3.4.

Вона ж слугуватиме для подальшого аналізу.

Використовуючи стандартну функцію ЛИНЕЙН категорії "Статистичні функції електронної таблиці Excel, отримуємо наступне рівняння:

Таблиця 3.4. Початкові дані для оцінювання параметрів рівняння множинної регресії

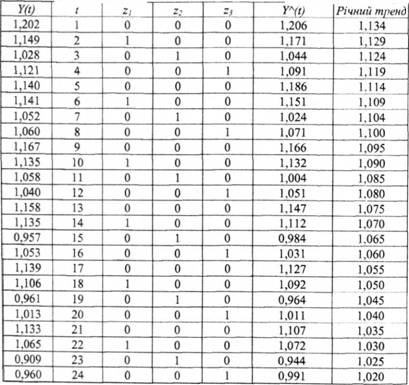
У дужках під оцінками параметрів розміщено їх помилки. Коефіцієнт детермінації R² = 0,906861.

Економетричний аналіз рівняння (3.14) дозволяє зробити такі висновки. По-перше, за t- критерієм Стьюдента лише оцінка " -0,02989" при фіктивній змінній z1 є не значимою, інші оцінки - значимі. По-друге, значення коефіцієнта детермінації і результати перевірки гіпотези щодо адекватності моделі в цілому за допомогою

F- критерію Фішера вказують на адекватність (працездатність моделі), що є доброю передумовою подальшого застосування моделі (наприклад, здійснення прогнозних розрахунків). По-третє, знаки при оцінках параметрів указують на наступну загальну закономірність: із плином часу і врахованих сезонних ефектах ножиці між витратами й доходами населення зменшуються (правда нерівномірно немонотонно в кожному кварталі). Як наслідок величина фінансової небезпеки регіону (навіть, якщо вона невідома) зменшується.

Щоб завершити аналіз сезонних ефектів, наведемо окремі рівняння для кожного кварталу:

Усереднюючи їх, отримуємо річний тренд:

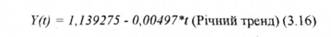
Відстань між лінією регресії кожного кварталу і річним трендом дає оцінку сезонної складової компоненти кожного кварталу (відповідні розрахунки наведені в додатку М):

Останній рядок є контрольним і вказує на коректність розрахунків.

Наведемо (макро)економічну інтерпретацію отриманих результатів. По-перше, бачимо зростання значень коефіцієнтів сезонності від одного кварталу до наступного. По-друге, вони (значення) в першому півріччі від'ємні, в другому - додатні. По-третє, (випливає з другого) в першому півріччі має місце "накопичення" доходів населення (в тому числі тіньових) на тлі невеликих витрат, у другому - переважають витрати над доходами (за рахунок попереднього накопичення). Але в цілому можна констатувати збільшення фінансової стабільності в регіоні й, відповідно, зменшення стану фінансової небезпеки.

Далі скористаємось графічним представленням (рис. 3.3).

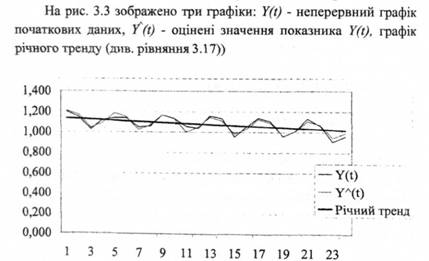
Рис. 5.3 Множинна регресія та річний тренд показника "відношення витрат до доходів населення"

Як бачимо, величина коефіцієнта детермінації замала. Це є ще одним підтвердженням необхідності застосування більш складних (більш адекватних) моделей.

Порівнюючи початкові дані з оціненими за допомогою рівняння множинної регресії (рис. 3.2), можна ще раз зробити висновок про працездатність пропонованої моделі (3.1) і можливість її використання з метою побудови прогнозів.

Виконаємо прогноз значень показника "відношення витрат до доходів населення" на 2007-2008 роки Для цього застосуємо рівняння (3.2). Результати прогнозних розрахунків наведено в таблиці 3.5

Прогноз показує майбутнє зменшення різниці між витратами і доходами населення приблизно на 2-4 % відсотка. Це дає підстави стверджувати про покращення фінансового стану регіону прямо пропорційно наведеним відсоткам.

Таблиця 3.5. Прогноз значень показника " відношення витрат до доходів населення Харківського регіону" на 2007-2008 роки

Оскільки система показників фінансової системи регіону не обмежується розглянутим показником, пропонується виконання подібного аналізу для показника "індекси споживчих сил".

Розглядаючи місячні дані значень показника "індекси споживчих цін" із 2001 року, можна простежити, що максимальний їх спад відбувається в серпні, а максимальне зростання в жовтні (див. рис. 3.4).

Рис. 3.3 дозволяє висунути припущення про наявність сезонних коливань показника "індекси споживчих цін". Графік автокореляційної функції представлено на рис. 3.4.

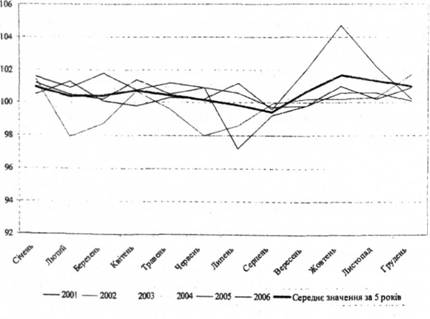
Рис. 3.4. Значення показника "індекси споживчих цін"з 2001 по 2006роки в місячному розрізі

З графіка можна зробити висновок про наявність тренду і лагових значень τ = 1, 3, 5, 7. Тобто можна висунути гіпотезу про специфікацію рівняння у вигляді:

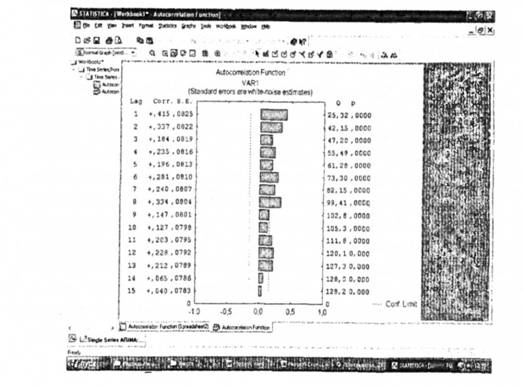
Рис. 3.5 Автокореляційна функція показника "індекси споживчих цін"

У ній всі оцінки параметрів значимі за t-критерієм, модель є адекватною за F-критерієм. Тобто можна вважати модель працездатною.

Дамо економічну інтерпретацію отриманому результату. Індекс споживчих цін у цілому зменшується з урахуванням плину часу (друга складова має знак "мінус"). Зменшення відбувається на тлі лагового впливу попередніх значень чинника. Цей вплив досягає + 0,346358 частини попереднього значення чинника х(ї~1). Звідси можна зробити висновок про зменшення фінансової небезпеки регіону. Графік теоретичної регресії фактично є згладженням фактичних даних подібно авто регресійним співвідношенням.

Показник "індекс споживчих цін" є предметом численних досліджень різними науковими дисциплінами. Метою цього дослідження є визначення прогнозних властивостей показника "індекс споживчих цін". Зокрема, істотними слід уважати виконання передпрогнозного аналізу із застосуванням методів фрактального аналізу. Під терміном "фрактальний аналіз" розуміється сукупність методів (методик), які досліджують самовіднесеність, самоподібність явищ, процесів, подій. Часові ряди мають статистичну само-подібність у часі. Е. Петерс наводить цікавий приклад часового ряду щоденного, тижневого й місячного ринкового прибутку [76, с. 69]. Без знання масштабу вимірів у трьох випадках розрізнити їх практично неможливо. Він стверджує, що фрактальні часові ряди - зміщені випадкові блукання.

Метою цього дослідження є передпрогнозний аналіз часового ряду показника "індекс споживчих цін". До нього (передпрогнозного аналізу) залучаються наступні етапи:

^ оцінка наявності та глибини довгострокової пам'яті;

^ визначення показника Херста Н;

^ виявлення трендостійкості або зворотної властивості, тобто "повернення до середнього частіше, ніж випадкова поведінка часового ряду" (реверс типу спаданням - підйом);

^ виявлення (періодичних) циклів, якщо вони є або квазицикл ів.

Знання наведених фрактальних характеристик досліджуваного часового ряду дозволить виявити прогнозні властивості часового ряду і, можливо, відібрати найліпший метод прогнозування з метою побудови сталого прогнозу.

Обчислювальна схема методу нормованого розмаху Херста наведена в монографії.

Застосовуючи обчислювальний алгоритм методу нормованого розмаху Херста до часового ряду показника "індекс споживчих цін" отримуємо наступні результати (табл. 3.6; рис. 3.6).

Таблиця 3.6. Розрахункові дані, отримані методом нормованих розмахів Херста

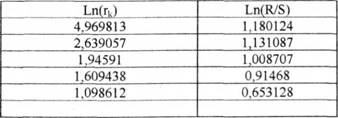
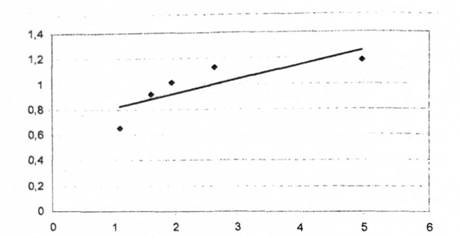
Рис. 3.6. Графік лінії за даними таблиці 3.6.

Показник Херста H дорівнює 0,1107. Він менший ніж 0,5. Тому цей ряд є персистентним (ергодичним). Подібну поведінку ряду називають "повертанням до середнього значення". Цей висновок підтверджується методом зворотних точок Кендела [76, с. 158]. У нашому випадку розрахунок дає 84 зворотних точки. Тобто він (інтервал) накриває число 84, але воно є близьким до лівого кінця певного інтервалу, що підтверджує результат попереднього фрактального аналізу. Загальний висновок полягає у твердженні про відсутність тренду часового ряду показника "Індекс споживчих цін".

Прогнозування стану фінансової системи регіону неможливо здійснити відповідно до класифікації пропонованої методики оцінювання, оскільки невідомо, які будуть порогові значення показників, що досліджуються в майбутньому. Прогнозувати значення граничних показників неможливо через відсутність їх статистичних даних минулого. Є такі показники, порогові значення яких є константою - це, як правило, показники що відображають відношення. В цьому випадку маємо "відношення витрат до доходів населення" та "індекси споживчих цін". За статистичними даними показників можна спрогнозувати стан фінансової системи порівняно з минулим через економетрична модифікація методу багатовимірної лінійної екстраполяції.

Модифікація методу багатовимірної лінійної екстраполяції дає можливість визначити закономірність поведінки результативного показника залежно від дії системи показників [76, с. 158]. Для використання модифікації цього методу наведемо необхідну термінологію і позначення. Під станом фінансової системи регіону S будемо розуміти кількісний опис відповідного об'єкта досліджень за допомогою двох систем чинників: факторних і результативних.

Діяльність регіону відбувається протягом деякого інтервалу часу [0,Т], де Т > 0. Таким чином, стан його фінансової системи змінює зовнішнє середовище. Ці зміни відображають ланцюг станів фінансової системи регіону

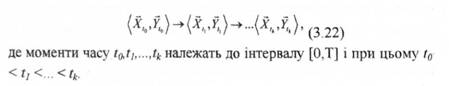
За допомогою таблиці 3.7 інформаційне відображені зміни станів фінансової системи регіону (див. ланцюг (3.7)).

Таблиця 3.7. Характеристика динаміки фінансового стану регіону

Оцінюючи стан фінансової системи Харківської області за запропонованою методикою станом на 2006 рік, [76] визначив, що він оцінений як безпечний.

Ураховуючи прогнозування значення показників фінансової системи Харківської області й модифікації методу багатовимірної лінійної екстраполяції, автор прийшов до висновку, що стан фінансової системи Харківської області в майбутньому (2007-2008 рр.) буде також оцінюватись як безпечний.