Теорія економічного аналізу - Купалова Г.І. - 12.4. Кластерний аналіз

Кластерний аналіз з'явився порівняно недавно – у 1939 р. Його запропонував вчений К. Тріон. Дослівно термін "кластер" в перекладі з англійської "cluster" означає гроно, згусток, пучок, група.

Особливо бурхливий розвиток кластерного аналізу відбувся у 60-х роках минулого століття. Передумовами цього були поява швидкісних комп'ютерів та визнання класифікацій фундаментальним методом наукових досліджень.

Кластерний аналіз – це метод багатомірного статистичного дослідження, до якого належать збір даних, що містять інформацію про вибіркові об'єкти, та упорядкування їх в порівняно однорідні, схожі між собою групи.

Отже, сутність кластерного аналізу полягає у здійсненні класифікації об'єктів дослідження за допомогою численних обчислювальних процедур. В результаті цього утворюються "кластери" або групи дуже схожих об'єктів. На відміну від інших методів, цей вид аналізу дає можливість класифікувати об'єкти не за однією ознакою, а за декількома одночасно. Для цього вводяться відповідні показники, що характеризують певну міру близькості за всіма класифікаційними параметрами.

Мета кластерного аналізу полягає в пошуку наявних структур, що виражається в утворенні груп схожих між собою об'єктів – кластерів. Водночас його дія полягає й у привнесенні структури в досліджувані об'єкти. Це означає, що методи кластеризації необхідні для виявлення структури в даних, яку нелегко знайти при візуальному обстеженні або за допомогою експертів.

Основними завданнями кластерного аналізу є:

– розробка типології або класифікації досліджуваних об'єктів;

– дослідження та визначення прийнятних концептуальних схем групування об'єктів;

– висунення гіпотез на підставі результатів дослідження даних;

– перевірка гіпотез чи справді типи (групи), які були виділені певним чином, мають місце в наявних даних.

Кластерний аналіз потребує здійснення таких послідовних кроків:

1) проведення вибірки об'єктів для кластеризації;

2) визначення множини ознак, за якими будуть оцінюватися відібрані об'єкти;

3) оцінка міри подібності об'єктів;

4) застосування кластерного аналізу для створення груп подібних об'єктів;

5) перевірка достовірності результатів кластерного рішення.

Кожен з цих кроків відіграє значну роль у практичному здійсненні аналізу.

Визначення множини ознак, які покладаються в основу оцінки об'єктів (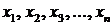), у кластерному аналізі є одним із найважливіших завдань дослідження. Мета цього кроку повинна полягати у визначенні сукупності змінних ознак, яка найкраще відображає поняття подібності. Ці ознаки мають вибиратися з урахуванням теоретичних положень, покладених в основу класифікації, а також мети дослідження.

При визначенні міри подібності об'єктів кластерного аналізу використовуються чотири види коефіцієнтів: коефіцієнти кореляції, показники віддалей, коефіцієнти асоціативності та ймовірносні, коефіцієнти подібності. Кожен з цих показників має свої переваги та недоліки, які попередньо потрібно врахувати. На практиці найбільшого розповсюдження у сфері соціальних та економічних наук здобули коефіцієнти кореляції та віддалей.

В результаті аналізу сукупності вхідних даних створюються однорідні групи у такий спосіб, що об'єкти всередині цих груп подібні між собою за деяким критерієм, а об'єкти з різних груп відрізняються один від одного.

Кластеризація може здійснюватися двома основними способами, зокрема за допомогою ієрархічних чи ітераційних процедур.

Ієрархічні процедури – послідовні дії щодо формування кластерів різного рангу, підпорядкованих між собою за чітко встановленою ієрархією. Найчастіше ієрархічні процедури

здійснюються шляхом агломеративних (об'єднувальних) дій. Вони передбачають такі операції:

– послідовне об'єднання подібних об'єктів з утворенням матриці подібності об'єктів;

– побудова дендрограми (деревоподібної діаграми), яка відображає послідовне об'єднання об'єктів у кластери;

– формування із досліджуваної сукупності окремих кластерів на першому початковому етапі аналізу та об'єднання всіх об'єктів в одну велику групу на завершальному етапі аналізу.

Ітераційні процедури полягають в утворенні з первинних даних однорівневих (одного рангу) ієрархічно не підпорядкованих між собою кластерів.

Одним із найбільш поширених способів проведення ітераційних процедур ось уже понад сорок років виступає метод k-середніх (розроблений у 1967 р. Дж. МакКуіном). Застосування його потребує здійснення таких кроків:

– розділення вихідних даних досліджуваної сукупності на задану кількість кластерів;

– обчислення багатовимірних середніх (центрів тяжіння) виділених кластерів;

– розрахунку Евклідової відстані кожної одиниці сукупності до визначених центрів тяжіння кластерів та побудова матриці відстаней, яка ґрунтується на метриці відстаней. Використовують різні метрики відстаней, наприклад: Евклідова відстань (проста і зважена), Манхеттенська, Чебишева, Мінковського, Махалонобіса 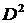тощо;

– визначення нових центів тяжіння та нових кластерів.

Найбільш відомими та широко застосовуваними методами

формування кластерів є:

– одиничного зв'язку;

– повного зв'язку;

– середнього зв'язку;

– метод Уорда.

Метод одиничного зв'язку (метод близького сусіда) передбачає приєднання одиниці сукупності до кластера, якщо вона близька (знаходиться на одному рівні схожості) хоча б до одного представника цього кластера.

Метод повного зв'язку (далекого сусіда) вимагає певного рівня подібності об'єкта (не менше граничного рівня), що передбачається включити у кластер, з будь-яким іншим.

Метод середнього зв'язку ґрунтується на використанні середньої відстані між кандидатом на включення у кластер і представниками наявного кластера.

Згідно методу Уорда приєднання об'єктів до кластерів здійснюється у випадку мінімального приросту внутрішньогрупової суми квадратів відхилень. Завдяки цьому утворюються кластери приблизно одного розміру, які мають форму гіперсфер.

Оптимальною прийнято вважати кількість кластерів, яка визначається як різниця кількості спостережень і кількості кроків, після якої відстань об'єднання збільшується стрибкоподібно.

Кластерний аналіз, як і інші методи вивчення стохастичного зв'язку, вимагає численних складних розрахунків, які краще здійснювати за допомогою сучасних інформаційних систем, зокрема з використанням програмного продукту Statistica 6.0.

Дослідники застосовують кластерний аналіз в різноманітних дослідженнях, наприклад при вивченні рівня добробуту населення країн СНД (О. Мірошниченко). Спочатку для цього було відібрано 16 статистичних основних соціально-економічних показників, які характеризують рівень життя громадян у різних країнах СНД:

1) ВВП у розрахунку на одну особу, дол. США;

2) середньомісячна номінальна заробітна плата, рос. руб.;

3) середньомісячний розмір пенсії, рос. руб.;

4) індекс інвестицій в основний капітал, процентів;

5) індекс споживчих цін, процентів;

6) частка витрат на купівлю продуктів харчування у споживчих витратах домогосподарств, процентів;

7) споживання м'яса та м'ясопродуктів у середньому за рік у розрахунку на одну особу, кг;

8) кількість пшеничного хліба, що можна було б придбати на суму середнього наявного грошового доходу за місяць (на одну особу), кг;

9) загальний коефіцієнт народжуваності (на 1000 осіб наявного населення);

10) коефіцієнт дитячої смертності (померло дітей віком до одного року на 1000 народжених);

11) число зайнятих у відсотках до економічно активного населення;

12) забезпеченість населення житлом у середньому (на одну особу), м2 загальної площі;

13) кількість хворих на злоякісні новоутворення (на 100 000 населення), осіб;

14) кількість зареєстрованих злочинів (на 100 000 населення), од.;

15) викиди шкідливих речовин в атмосферу стаціонарними джерелами забруднення (на одну особу), кг;

16) відвідування музеїв у середньому за рік (на 1000 населення), од. (табл. 12.7).

Кратерний аналіз здійснюється на основі співмірних та односпрямованих показників. Тому показники вхідної матриці слід спочатку стандартизувати. Одним із поширених способів для неоднорідних сукупностей (зокрема у нашому прикладі) є стандартизація показників шляхом відношення відхилення 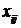- а до одиниці стандартизації q. У цьому випадку одиницею стандартизації буде фактичний варіаційний розмах .

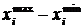При цьому, як показано у наукових працях учених-економістів A.M. Єріної та С.С. Ващаєва, для показників-стимуляторів береться 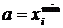, тим часом як для показників-дестимуляторів 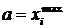. Виходячи з цього, стандартизовані значення показників розраховуються за формулами:

– для показників стимуляторів: ;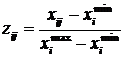

– для показників-дестимуляторів: .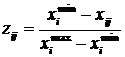

де 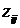– стандартизоване значення i-ro показника для у-ї одиниці сукупності, , ;

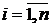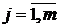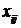– вхідне значення і-го показника для j-ї одиниці сукупності.

Отримані стандартизовані вхідні дані представлені в табл.12.8.

* Тут і далі наведені результати кластерного аналізу, проведеного О.Ю. Мірошниченко.

Таблиця 12.8. Матриця стандартизованих вхідних даних

Наступним кроком кластерного аналізу повинна бути побудова матриці відстаней, що передбачає насамперед вибір метрики відстаней. На практиці застосовують різні метрики відстаней: Евклідова, зважена Евклідова, Манхеттенська, Чебишева, Мінковського, Махалонобіса D² та ін. В даному випадку розподіл країн СНД на групи можна здійснити за допомогою Манхеттенської відстані. Вона розрахована за формулою

,

де 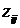та 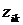– стандартизовані значення і-го показника j-ї та k-ї одиниць сукупності.

Виходячи з обраної міри відстаней, можна побудувати симетричну матрицю відстаней між країнами СНД (табл. 12.9).

Наступним етапом аналізу є вибір методу об'єднання країн СНД у кластери. Як уже зазначалося, найпоширенішими методами формування кластерів є:

– одиничного зв'язку;

– повного зв'язку;

– середнього зв'язку;

– метод Уорда.

Скористаємося методом Уорда, який дає змогу мінімізувати внутрішньогрупову дисперсію всередині кластерів. Згідно з цим методом, приєднання об'єктів до кластерів здійснюється за мінімального приросту внутрішньогрупової суми квадратів відхилень. Це сприяє утворенню кластерів приблизно однакового розміру, які мають форму гіперсфер. Дендрограму результатів кластерного аналізу зображено на рис 12.5.

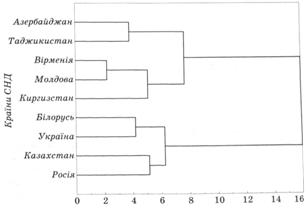
Рис. 12.5. Дендрограма результатів кластерного аналізу країн СНД за рівнем життя населення

Як видно з рисунка, вертикальна вісь дендрограми відображає країни СНД, а горизонтальна є відстанню об'єднання.

З метою визначення оптимальної кількості кластерів слід побудувати графік списку об'єднання регіонів України у кластери, відклавши на вертикальній його осі відстані, а на горизонтальній – крок об'єднання (рис. 12.6).

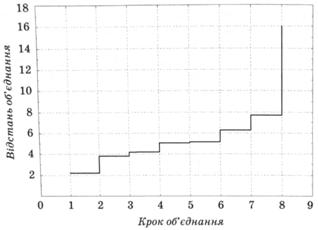
Рис. 12.6. Графік списку об'єднання країн СНД у кластери

Як бачимо оптимальним, згідно з встановленими вимогами оптимальності, є розбиття країн СНД за рівнем життя населення на три кластери. Зазначимо, що оптимальною вважається така кількість кластерів, яка дорівнює різниці кількості спостережень (у нашому прикладі – 9) і кількості кроків, після яких відстань об'єднання зростає стрибкоподібно (у нашому прикладі – 6).

Таким чином, країни СНД розподілено на три кластери. До першого кластера увійшли: Азербайджан і Таджикистан, до другого – Білорусь, Україна, Росія та Казахстан, і третього – Вірменія, Молдова і Киргизстан.

За допомогою методу k-середні обчислені середні значення показників для кожного з трьох кластерів (рис. 12.7).

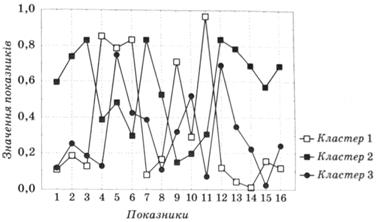
Рис. 12.7. Середні значення показників для кожного кластера

Як зображено на рис. 12.7, до першого кластера входять країни, у яких середні значення восьми показників менші, ніж у інших кластерах.

Так, Азербайджан і Таджикистан, що належать до першого кластера, мають низькі показники ВВП на одну особу, середньомісячної заробітної плати (номінальної), пенсії, споживання м'яса та м'ясопродуктів, забезпеченості житлом. Проте у цих країнах вищі інші середні показники, зокрема: індекс інвестицій в основний капітал, індекс споживчих цін, коефіцієнт народжуваності .

Країни, віднесені до другого кластера, відзначаються найвищими параметрами економічної складової рівня життя, але, на жаль, низькою народжуваністю, вищим рівнем захворюваності на злоякісні новоутворення, злочинності, більшими викидами шкідливих речовин в атмосферу стаціонарними джерелами забруднення, що підтверджується відповідними показниками.

Країни третього кластера характеризуються найнижчими показниками: індексу інвестицій в основний капітал, рівня зайнятості населення в суспільному господарстві, зареєстрованих злочинів, що свідчить про їх низьку інвестиційну привабливість і значне безробіття.

Отже, кластерний аналіз, за оцінкою науковців, має велике значення в проведенні аналітичних досліджень завдяки можливості перетворити великий обсяг різнобічної інформації в упорядкований, компактний вигляд. Це сприяє підвищенню рівня наочності, зрозумілості та сприйняття результатів аналізу, а також створює підґрунтя для прогнозування.