Статистика - Опря А.Т. - § 1.2. Помилки при перевірці статистичних гіпотез. Статистичні критерії і критична область

Перевірка статистичних гіпотез здійснюється на основі вибіркових даних. Обмеженість обсягу вибірки зумовлює можливість прийняття неправильних рішень. Інакше кажучи, висунута гіпотеза може бути вірного і невірного. Звідси виникає необхідність перевірки правильності прийнятого рішення. Перевірку здійснюють статистичними методами, тому називають її статистичною перевіркою. В результаті такої перевірки існує можливість у двох випадках прийняти невірне рішення, тобто здійснити два роди помилок: або відхилити гіпотезу, коли вона вірна; або прийняти гіпотезу, коли вона невірна. їх називають відповідно помилками першого і другого роду. Таким чином, помилка першого роду полягає в тому, що нульова гіпотеза н₀ приймається в той час, як є вірною гіпотеза Ні. Схематично ці випадки наведено в таблиці 96.

Таблиця 96.

Помилки при статистичній перевірці гіпотези

У результаті перевірки статистичної гіпотези її або приймають, або відхиляють. З цієї метою використовують випадкову величину, розподіл якої відомий. Залежно від закону розподілу цю величину в математичній статистиці прийнято позначати: а) ї (абои)- якщо вона розподілена нормально; б^і⁷ - розподіл за законом Фішера-

Снеденора; в) ї (або Т)- за законом Стьюдента; г) %^г - за законом "Хі-квадрат" Пірсона і т.д.

Прийняте рішення відносно нульової гіпотези, 'таким чином, повинно опиратися на статистичні критерії. Під критерієм розуміють випадкову величину, на підставі якої приймається однозначне правило, що встановлює умови, при яких перевірювана гіпотеза повинна бути прийнята чи відхилена. Термін "прийняти гіпотезу" означає: "вирішити, що результати спостережень, не суперечать висунутій гіпотезі". Під терміном "відхилити гіпотезу" слід розуміти протилежне - "вирішити, що результати спостережень суперечать висунутій гіпотезі".

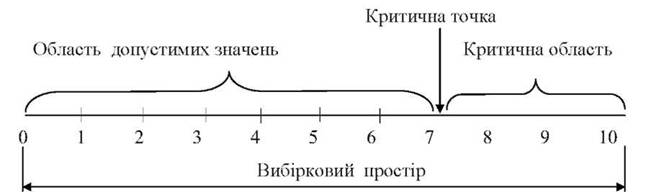
Рис. 39. Вибірковий простір випадкової змінної

Якщо уявити вибірковий простір як множину можливих вибіркових значень, розташованих у порядку зростання (рис.39), то статистичний критерій поділяє цей простір на дві непересічні області: критичну і область прийняття гіпотез (область допустимих значень, додаткова область). Точки, що відділюють критичну область від області прийняття гіпотези, називаються критичними точками (границями). Слід розрізняти односторонню (правосторонню і лівосторонню) і двостронню критичні області. Якщо прийняти позначення критерію через К, критичної точки - Кцр , то правосторонню критичну область можна уявити у вигляді нерівності к>к_кр (К_кр- додатне число). Лівостороння критична область визначається нерівністю К< К_кр (К^, - від'ємне число). Таким чином, одностороннью називають правосторонню або лівосторонню критичну область.

У випадках, якщо К < К_ь К > К₂ (при К₂ >Кі), критичну область називають двосторонньою.

На рис. 40 схематично зображено правосторонню (1), лівосторонню (2) і двосторонню критичну область (3).

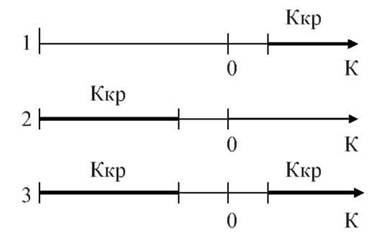
Рис. 40. Критична область: 1 - правостороння; 2 - лівостороння; 3 - двостороння

Якщо вибіркове значення статистичного критерію попадає у критичну область, то гіпотеза, яка перевіряється відхиляється, якщо у додаткову - гіпотеза приймається.

Отже, під критичною областю розуміється сукупність значень статистичної характеристики гіпотез, коли спостережуване значення характеристики належить до цієї сукупності, то гіпотеза Н₀ відхиляється на користь гіпотези Ні.

Область допустимих значень (додаткова) даного критерію - це множина допустимих положень вибіркової точки у вибірковому просторі, які призводять до прийняття нульової гіпотези.

Під вибірковою точкою у математичній статистиці розуміють конкретне значення досліджуваної величини х, одержане у даній вибірці.

Як говорилося раніше, при перевірці статистичної гіпотези існує можливість зробити два роди помилок.

У задачах перевірки гіпотез помилка першого роду носить назву рівня значимості (мала ймовірність). Рівень значимості - це ймовірність зробити помилку першого роду, тобто відхилити правильну гіпотезу. Із зменшенням рівня значимості зростає ймовірність помилки другого роду при одному й тому ж обсязі вибірки.У статистичній практиці застосовують 5%-й рівень значимості. Його прийнято позначати через а - або Р^_05; Р₀д і т.д.

Величина, що доповнює ймовірність помилки другого роду, називається потужністю критерію для перевірки гіпотези проти її альтернативи. Отже, потужність критерію - це ймовірність того, що нульова гіпотеза (Но) буде відхилена, якщо вірна конкуруюча /Ц/, тобто є ймовірність не допустити помилку другого роду. Потужність критерію може бути зображена графічно (рис.41), як приклад, тут розглянемо випадок, коли в умовах дії нульової гіпотези, яка складається в визнання оцінки ~ невідомого параметра х ,що дорівнює ~' при конкуруючій гіпотезі ~ = ~ " , вибіркова середня ~ розподілена нормально з щільністю ймовірностей /₀(г) .Критерій будується так, що він є функцією ~. При цьому х = 0; а¹ = 1.

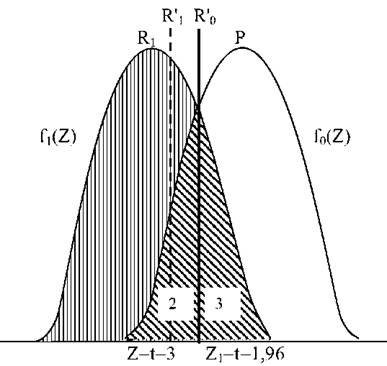
Рис. 41. Розподілу в умовах дії нульової і конкуруючої гіпотез: 1 - потужність критерію при даній альтернативі; 2 - імовірність помилки першого роду; 3 - імовірність помилки другого роду

Якщо справедлива конкуруюча гіпотеза, то критерій ї розподілений з щільністю ймовірностей Ц(ъ). У цьому випадку, наприклад, значення | Ц | > 1.96 зустрічається з імовірністю 0,05, а |ї| > 3-з імовірністю 0,003. Перпендикуляр Я₀ проведений з точки ъ , що дорівнює 1,96, поділяє площину на дві части Я₀ і Яі . Якщо обчислене значення X попадає у точки, які належать області Я₀ , то нульова гіпотеза (Но) не відхиляється.

Якщо значення ґ, попадає в область я₁ , то нульова гіпотеза відхиляється і приймається конкуруюча гіпотеза.

Перевірка нульової гіпотези (Н₀) здійснюється у такій послідовності:

1) вибирається рівень значимості;

2) визначають критичну область, яка відповідає цьому рівню значимості;

3 обчислюють вибіркове (фактичне) значення статистичної характеристики X ;

4) при попаданні значення ґ у критичну область нульова гіпотеза відхиляється; при попаданні X у область допустимих (додаткових) значень - гіпотеза не відхиляється.