Статистика - Опря А.Т. - § 1.5. Основні аспекти і умови застосування Xi - квадрат критерію

Хі - квадрат (критерій згоди Пірсона - %²) є об'єктивною оцінкою близькості емпіричних розподілів до теоретичних. Використовується, як уже було сказано, у тих випадках, коли необхідно встановити відповідність двох порівнюваних рядів розподілу - емпіричного і теоретичного, або двох емпіричних. При цьому порівнюються частоти названих рядів розподілу, виявляються розбіжності між ними і визначається вірогідність цих розбіжностей.

За допомогою Хі - квадрат критерію можна виявити відміни в розподілі двох емпіричних рядів, порівнювати вибірки, які мають альтернативні ознаки, а також оцінювати вірогідність кореляції між альтернативними ознаками. Як і інші критерії згоди (Колмогорова А, Романовского, Фішера Б, Ястремского Ь), х² являє собою деяку величину, яка оцінюється з певною ймовірністю. Він може приймати різні завжди додатні значення (малі й великі). При ^²=0 слід вважати, що відміни між частотами порівнюваних рядів розподілу відсутні. Даний критерій не рекомендується використовувати для оцінки малих вибірок.

Як було показано в § 1.4, за допомогою х² - критерію можна здійснити статистичну перевірку гіпотез відносно розподілів, тобто відповідність емпіричних даних розподілу деякому теоретичному закону розподілу. Таку оцінку наближення емпіричного розподілу до теоретичного дає сума співвідношень частот

де п_ф, п_т - відповідно частоти емпіричного і теоретичного ряду.

Збіг емпіричних і теоретичних частот зумовлює величину х¹ = 0. Це вказує на підтвердження нульової гіпотези. (Но). При наявності достовірної різниці у частотах емпіричного і теоретичного ряду величина х¹ буде свідчити про неправильність висунутої гіпотези.

Значення параметра ХІ - квадрат зростає із збільшенням різниці між частотами. Величина х² також залежить від числа ступенів вільності. Чим менше значення х², тим вищі його ймовірність і вірогідність. Таким чином, при зміні величини х² від 0 до а> імовірність його змінюється від 1 до 0. У міру наближення п к а> розподіл х² наближається до нормального.

При використанні ХІ - квадрат критерію необхідно пам'ятати про достатньо велике число одиниць вибірки (п > 50) і величини частот (п > 5). Як було сказано раніше при п, < 5 об'єднують сусідні інтервали ряду розподілу. Якщо вибіркова сукупність досить велика,

Хі - квадрат критерій буде обґрунтований, тобто у такому випадку він майже завжди спростовує невірну гіпотезу. Серед розроблених критеріїв згоди цей критерій забезпечує мінімальну помилку в прийнятті невірної гіпотези.

При оцінці відмінностей між емпіричним і теоретичним розподілами потрібно знати величини х¹ , які відповідають визначеним рівням значимості. Для цієї мети К.Пірсон розробив стандартні таблиці, в яких на перетині значень х¹ і числа ступенів вільності подані ймовірності, які оцінюють величину х¹ (додаток 6) .

Якщо за розрахунковими даними значення ймовірності виявиться дуже малою величиною, наприклад 0,01, то відмінності між досліджуваними рядами потрібно вважати істотними, тобто нульова гіпотеза не приймається. Якщо ж імовірність виявиться не малою, розбіжності вважаються випадковими і нульова гіпотеза приймається. Р.Фішер довів, що ризик зробити помилку буде невеликим, якщо провести суміжну лінію у ймовірності Р = 0,05. Значення х¹ , які лежать за цією лінією (0,04; 0,03; 0,02 тощо), .вказують на наявність істотних відхилень.

При розрахунку числа ступенів вільності досліджуваних частот враховують кількість обчислювальних статистичних характеристик теоретичної функції розподілу. У даному випадку використовувана кількість таких параметрів дорівнює 2 (~,<т) , звідси и =І-1- 2 .

Приклад. Розглянемо розрахунок оцінки відмінності теоретичного і емпіричного розподілів 54 підприємств за трудомісткістю виробництва одиниці продукції (табл. 100).

Для знаходження величини х^% використовується відома формула:

де п_;,п_т - відповідно емпірична і теоретична частоти ряду розподілу. У нашому прикладі, підсумовуючи часткові значення величин х^%, одержуємо розрахункове значення х² - критерію, що дорівнює 4,57. Знаходимо число ступенів вільності для даного випадку :и=І -1-р=6-1-2=3 (І = 6, оскільки два останні інтервали об'єднані в один). За стандартною таблицею /додаток. б/ знаходимо Р(х¹ =4,57) при числі ступенів вільності, рівному 3. Табличне значення Р( х¹ )= 0,1718. Даний рівень імовірності значно відрізняється від нуля. Тому відмінність між емпиричним і теоретичним розподілами потрібно вважати випадковою і досліджуваний розподіл підприємств за трудомісткістю одиниці продукції необхідно визнати як підпорядкований закону нормального розподілу.

Таблиця 100

Розрахунок критерію х¹ при оцінці відмінностей між емпіричним і теоретичним

рядами розподілу

Замість значень показників ймовірності (Р х²), розроблених К.Пірсоном, Р.Фішер розрахував стандартну таблицю значень х¹ , які відповідають шуканим імовірностям при різному числі ступенів вільності варіації (додаток. 7).

Розрахунок, такої стандартної таблиці він аргументував тим, що в практичних обчисленнях не так важливо знати точне значення ймовірності Р, яке відповідає значенню х², як визначити, в який мірі вірогідно фактичне значення х². Тому в стандартних таблицях Р.Фішера наведено значення х², які відповідають певним рівням імовірності Р х². При цьому потрібно відмітити, що названі таблиці містять значення ^²<1, які зустрічаються для малих ступенів вільності, і значення ^²>30 - для великих величин и .

Стандартні математичні таблиці значень х², Р. Фішера мають більш широкі аспекти практичного використання при розрахунках статистичних оцінок. Випадок їх використання при перевірці гіпотези про розподіли був розглянутий у § 1.4. Нижче викладені деякі інші аспекти розрахунку статистичних оцінок з застосуванням критичних значень х² стандартних таблиць Р.Фішера.

За допомогою критерію ХІ- квадрат можна перевірити належність кількох вибіркових даних однієї і тієї ж генеральної сукупності при вирішенні питання про однорідність вибірки.

Приклад. Порівняти варіаційний ряд продуктивності молочного стада корів ферм великого рогатої худоби з частковою механізацією і повною механізацією виробничих процесів.

Обчислення хі- квадрат критерію для встановлення різниці в частотах двох емпіричних рядів полягає в тім, що за частоти невідомої генеральної сукупності приймаються величини половини суми частот по кожному інтервалу порівнюваних рядів розподілу (табл. 101).

Подальші розрахунки зводяться до знаходження різниці емпіричних і теоретичних частот і визначення суми їх співвідношень по вже відомій формулі Хі - квадрат критерію (табл. 102).

При цьому в ряд емпіричних частот заносять у послідовному попарної запису частоти обох рядів, у графу теоретичних частот - відповідні їм усереднені частоти теоретичного ряду. Розраховані часткові значення х² підсумовують і

2 2

отриману суму ) порівнюють із стандартним значенням (%_т) при рівні

значимості а = 0,05 і числі ступенів вільності варіації и=І-1= 9-1=8 (додаток. 7). Як бачимо, критична точка для цих параметрів становить 15,5, тобто величина

22

%_т дорівнює 15,5 і менше % на 4,4 при порозі імовірності Р = 0,95.

Таблиця 101

Розрахунок теоретичних частот при порівнянні двох емпіричних рядів

Таблиця 102

Розрахунок значення критерію %^{г П}Р^И порівнянні двох емпіричних рядів

Оскільки %² > ^ можна зробити висновок про вірогідність різниці двох

емпіричних рядів за показниками продуктивності молочного стада корів. Як видно, стан механізації виробничих процесів суттєво впливає на показники продуктивності тварин які обслуговуються . А вибіркову сукупність поголів'я корів, з обслуговуванням при повній механізації процесів, слід вважати якісно іншою- вона належить до другої генеральної сукупності.

У порівнянні із способом обчислення величини Хі -квадрата, розглянутого раніше (в §1.4), коли мова йшла про порівняння емпіричного і теоретичного ряду, в даному прикладі значення %

занижено майже в два рази. Це зумовлюється прийнятим способом обчислення, коли при обробці даних використовується не різниця частот, а напіврізниця, і кількість величин часткових значень х¹ більша в два рази, ніж в розрахунках розбіжностей емпіричного і теоретичного рядів розподілу.

При порівнянні двох емпіричних рядів розподілу, представлених неоднаковою кількістю одиниць вибіркової сукупності (Іп₁^Іп₂),

розрахунок ХІ - квадрат критерію має свою особливість

Приклад. Потрібно визначити, чи вірогідна розбіжність частот за показниками врожайності зернових культур в інтервальному ряді розподілу підприємств з посівами озимої і ярої пшениці (табл. 103).

Таблиця 103

Розрахунок теоретичних частот при порівнянні двох емпіричних рядів з нерівною кількістю одиниць спостережень

На першому етапі розрахунків визначають теоретичні частоти для двох емпіричних рядів (табл. 104), суми за якими повинні бути рівні сумам частот

відповідних рядів(Т.п, = Еп_п = п_т2).Потім розраховують часткові значення %^г за раніше описаною схемою і одержані значення підсумовують (табл. 104).

₂

Розрахункова величина хі - квадрат критерію ) в розглянутому прикладі

дорівнює 8,39. Число ступенів вільності у = (І₁ - 1)(І₂ -1) , де І₁ -число інтервалів, І₂ - число емпіричних рядів розподілу. Таким чином, і)=(5-1)(2-1)=4. За стандартною таблицею значень %^г (додаток 7) знаходимо теоретичне значення

хі- квадрат критерію ( ^²) .

Для порогу ймовірності Р =0,95 і числа ступенів вільності 4 величина

₂₂

його становить 9,5. Оскільки % > % можна зробити висновок про неістотність

різниці в частотах двох емпіричних рядів розподілу, які являють собою неоднакову вибірку за кількістю одиниць спостереження.

Таблиця 104

Розрахунок значення критерію %^{г П}Р^И порівнянні двох емпіричних рядів з нерівною кількістю одиниць спостережень

Хі - квадрат критерій використовується також при порівняні двох альтернативах розподілів, представлених у вигляді кореляційної решітки. Формула, за якою обчислюється х¹ , ^в цьому випадку має вигляд:

(аа¹ - вс)--п

2 І 2 ]

X ⁼---_,

(а + е)(с + а )(а + с)(е + а)

де а,в,с,а- частоти у відповідних клітинах кореляційної решітки;

п - число одиниць вибіркової сукупності. Для прикладу розглянемо таблицю розподілу робітників по двох групах альтернативних ознак (табл. 105).

Після підстановки у наведену вище формулу даних таблиці 105 одержимо:

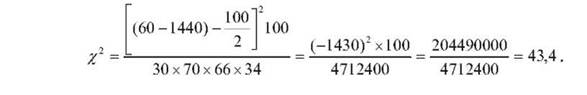
Таблиця 105

Розрахунок значення %^{г П}Р^И порівнянні альтернативних розподілів

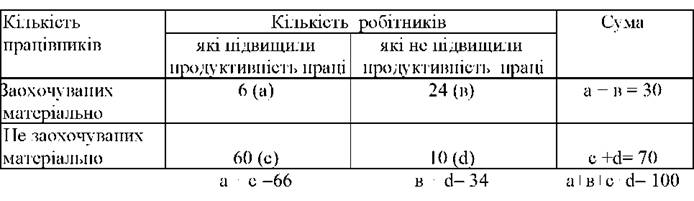
Число ступенів вільності у = (І - 1)(І₂ - 1) =(2-1)(2-1)=1 (І₁.І₂- число груп відповідно по першій і другій ознаках). Отримане розрахункове

значення Хі - квадрат критерію (%_Р^г) порівнюємо з табличним значенням (додаток 7).

Для порогу ймовірності 0,95 величина його становить 3,8. Оскільки £ > £_т (43,4 > 3,8), можна зробити висновок, що

розглядувані альтернативні розподіли різняться значимо, тобто матеріальний стимул зумовлює підвищення продуктивності праці робітників.

Одне із практичних значень Хі - квадрат критерію полягає у тому, що розрахункову його величину при альтернативних ознаках (% ) можна використовувати для визначення ступеня тісноти зв'язку

між ними. Такою статистичною характеристикою є коефіцієнт кореляції (г_х).Розрахунок його проводиться за такою формулою:

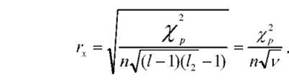
Для прикладу, розглянутого вище, величина коефіцієнта

43,4

кореляції становитиме: г_х =1 400^4 = ,434 = 0,659.

По його рівню можна стверджувати про досить значний ступінь тісноту зв'язку між продуктивністю праці і її матеріальним стимулюванням.

Крім розглянутих випадків Хі- квадрат критерій може бути застосований і для других розподілів, в яких розбіжності між теоретичними (очікуваними) і фактичними частотами не відповідають якій-небудь очевидній структурі. Використовують даний критерій згоди і при з'ясуванні об'єктивності побудови ряду розподілу, тим самим виключаючи можливість підгонки одиниць спостереження з метою відповідності їх одна одній.

Проте, використання цього критерію передбачає ряд обмежень , яких необхідно дотримуватись при розрахунку х^{2 як} критерію істотності. Як було відмічено раніше, при перевірці гіпотези на відповідність емпіричного розподілу теоретичному бажано мати не менше 50 одиниць спостереження, а в кожній теоретично розрахованій групі мінімально допустима границя величини частот умовно приймається рівною 5 (інколи 3). У зв'язку з цим при малочисельності груп (як правило, крайніх) їх об'єднують. При визначенні відповідності розподілів нормальному закону число ступенів вільності дорівнює числу груп (інтервалів) мінус три (/ - 3). Пояснюється це тим, що обчислення теоретичних частот пов'язано тут трьома умовами (обмеженнями), які визначають нормальний розподіл: визначеним обсягом вибірки (п), середньою величиною (~), від якої знаходяться центральні відхилення, середнім квадратичним відхиленням (сг), за яким проводиться нормування центральних відхилень серед груп (інтервалів).

При об'єднанні інтервалів (у випадку наявності в ряді розподілу частот нижче мінімально допустимого рівня) число ступенів вільності коригують. Величина вторинного числа ступенів вільності дорівнюватиме різниці між числом інтервалів після їх об'єднання мінус 3 (І' -3). Тому для прикладу, розглянутого в § 1.4., останніх два інтервали потрібно було об'єднати. У зв'язку з цим число ступенів вільності становитиме и=І - 3 = 7-3=4.

При цьому стандартне значення Хі- квадрат критерію для Р = 0,95 дорівнюватиме 9,5 (додаток 7).

Розглянуті вище випадки використання Хі - квадрат критерію свідчать про широкі можливості його застосування в практиці статистико - економічного аналізу.