Статистика - Опря А.Т. - § 1.6. Оцінка розподілів з використанням критерію згоди Колмогорова

Розглянуті в попередніх параграфах способи оцінки відмінності між двома вибірковими спостереженнями ґрунтувалися на припущенні про нормальний характер розподілу генеральних сукупностей (або близькому до нормального). Але експериментатору (досліднику) не завжди відома форма розподілу даних, з яких проводиться вибірка. Тому використання критеріїв X і х¹ може інколи привести до суб'єктивної оцінки результатів спостережень. У зв'язку з цим в математичній статистиці розроблені критерії оцінки вибірок з будь - якого виду розподілу.

Теоретичною основою їх розробки є припущення, що ряд послідовних спостережень можна розглядати як просту незалежну вибірку з незмінним розподілом. Ці критерії одержали назву непараметричних. Для їх розрахунків непотрібно обчислювати середню, дисперсію та інші статистичні характеристики вибіркових розподілів. У деяких випадках для розрахунку непараметричних критеріїв використовуються не безпосередні дані спостереження, а різного роду впорядковані ряди (з нагромадженими частотами, ранжировані різниці одиниць спостережень і т.п.). Критерії, які розраховуються у цьому випадку, називають порядковими.

До непараметричних критеріїв відносять: критерій Л, (ламбда) Колмогорова, критерій Уайта, критерій Уілксона.

Ступінь наближення емпіричного розподілу до обчислюваного (теоретичного), в равній мірі як і порівняльну оцінку двох однорідних варіаційних рядів, визначають за допомогою непараметричного критерію Л (ламбда). Якщо використання хі- квадрат критерію ґрунтується на використанні таких вибіркових характеристик (параметрів) як середня (5с) і стандарт (а), то при розрахунку Л -критерію їх обчислення непотрібно. Він оснований на відповідності рядів інтегральних (нагромаджених) частот досліджуваних сукупностей. Суть його полягає в розрахунку величини максимальної різниці (D) нагромаджених частот (частостей) емпіричного і теоретичного розподілів. Тобто для використання цього критерію необхідне впорядкування двох рядів розподілу у вигляді їх кумуляції. А.Н.Колмогоров довів, що при необмеженому зростанні чисельності вибірки (n) імовірність нерівності Dyfn >Х прямує до границі

limРф4П >х) = і£ (-1)^к е-^2Л

де D - величина максимальної різниці нагромаджених частот (частостей) емпіричного і теоретичного розподілів.

Непараметричний показник X розраховується як відношення максимальної різниці (без врахування її знака) нагромаджених частот емпіричного і теоретичного рядів розподілу до кореня квадратного із чисельності вибірки:

D ^max| n_i - n_T І

У випадку повного збігу порівнюваних частот в рядах розподілу X = 0. Чим більша розбіжність в рядах, тим більша величина ламбда-критерію. Але занадто велику величину X випадковими відхиленнями у порівнюваних рядах розподілу пояснити важко, тому робиться висновок про невідповідність вибіркового розподілу і теоретично припущеного.

Критерій згоди Колмогорова (а), на відміну від Хі- квадрат критерію, дуже простий не тільки в розрахунках, але й не передбачає використання стандартних таблиць для його оцінки. Теоретично доведено, що при чисельності вибіркової сукупності приблизно більш 25 одиниць (n > 25) граничні значення критерію ламбда (Х_І), що відповідають трьом порогам довірчої імовірності (Р = 0,95; Р = 0,99; Р= 0,999), дорівнюють відповідно 1,36; 1,63; 1,95. Показник числа ступенів вільності при цьому не розраховується.

Таким чином, якщо л_р >х_т, то з відповідною ймовірністю розбіжності між емпіричним і теоретичним розподілами визнаються значущими (істотними).

Приклад. Продемонструємо розрахунок критерію згоди Колмогорова на прикладі розподілу підприємств за урожайністю зернових культур (табл. 106).

Таблиця 106

Розрахунок критерію "ламбда" (X ) при оцінці розбіжностей між емпіричним і теоретичним

рядами розподілу

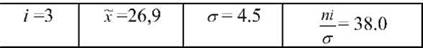
Максимальне значення різниці нагромаджених частот емпіричного і теоретичного рядів розподілу дорівнює " - гіт ^{= 5} ■ Величина ламбда-критерію становитиме:

Х=-⁵= = 0,66.

Одержана величина критерію (0,66) значно менше теоретичного її рівня (Л₀5⁼ 1,36) відповідного порога ймовірності (Р = 0,95). Тому розходження між емпіричним розподілом і нормальним визнаються невірогідними, тобто розходження між частотами знаходяться в межах випадкових коливань.

Для виявлення вірогідності двох емпіричних розподілів, одержаних в результаті вибірки з однієї і тієї ж генеральної сукупності, але які мають неоднакову кількість одиниць, критерій "ламбда" обчислюється за формулою:

Би, Щ, и,и,

X = -¹--- max -

Би,

де -¹ - суми нагромаджених частот по кожному інтервалу першого ряду гі

розподілу, поділені на обсяг вибірки;^"і - _те ж по другому ряду розподілу;

^гі. _ Zrii max - максимальне абсолютне значення (без врахування знака)

різниці часток від ділення нагромаджених частот на обсяг вибірки;

и₁, и₂ - обсяги одиниць вибіркової сукупності по першому і другому ряду розподілів.

У таблиці 107 представлені два емпіричних ряди розподілу підприємств за врожайністю зернових культур, відібраних з однієї генеральної сукупності, але які різняться обсягами вибірки.

В останній графі цієї таблиці максимальна різниця кумульованих частот

представлена величиною 0,07. Підставивши її у вище наведену формулу,

знайдемо значення критерію "ламбда".

Ггі1хгі7 _пг7 /100 х 200 " _ґп

Х = d max Р-^ = 0.07,-= 0,57 .

₁+ n₂ V 100 + 200

Розрахована величина критерію менше граничних критичних значень X для всіх трьох порогів імовірності (Л₀₀₅ = 1,36; 1_{0 01} = 1,63; 1_{0 001} = 1,95). Це свідчить

про неістотність розбіжностей між порівнюваними емпіричними рядами розподілу. Звідси висновок про те, що обидві вибірки репрезентують досліджувану генеральну сукупність.

У випадках, коли під знаком радикала громіздкі числа, розглянуту вище формулу приводять до вигляду:

X^і = d² max ril^ri..

П + n₂

Таблиця 107

Розрахунок критерію "ламбда" {X >при оцінці розбіжностей між емпіричними рядами розподілу з

неоднаковими обсягами вибірки

Підставивши в цю формулу необхідні значення, маємо:

* ₌ о,07^22000- ₌ 0,327; 300

X = ^0,327 = 0,57.