Рядом динаміки називається ряд чисел, що характеризує зміну суспільних явищ у часі. Фактично це сукупність значень показника, розміщених у певному хронологічному порядку. Прикладом ряду динаміки можуть бути дані, наведені в табл.10.17.
Таблиця 10.17. Чисельність фахівців вищої кваліфікації в Україні станом на 1 жовтня 2000–2005 pp., осіб
Науковий ступінь | 2000 | 2003 | 2004 | 2005 |
Доктор наук | 10 339 | 11259 | 11573 | 12 014 |
Кандидат наук | 58 741 | 64 372 | 65 839 | 68 291 |
Ряди динаміки – надзвичайно важливий метод аналізу, завдяки якому можна охарактеризувати зміну суспільно-економічних явищ у часі, виявити особливості, основні тенденції, закономірності їх розвитку, спрогнозувати їх на майбутнє та виразити у цифровій і графічній формах. Наприклад, аналіз показників динамічного ряду виробництва продовольчих товарів за кілька років дасть змогу простежити тенденцію зміни обсягу продукції, що свідчитиме про розвиток сільського господарства, харчової промисловості, рівня і культури споживання населення, а також технології виробництва.
Залежно від способу вираження рівнів (у вигляді абсолютних, відносних і середніх величин) ряди динаміки поділяються на ряди абсолютних (показники площ, товарообігу, виробництва і т. ін.), відносних (частка молодих працівників у загальній чисельності працюючих, показники виконання договірних зобов'язань, темп зростання обсягів інвестицій і т. ін.) і середніх величин (продуктивність праці, заробітна плата одного працівника, урожайність сільськогосподарських культур тощо).
У свою чергу ряди динаміки абсолютних величин поділяються на моментні та інтервальні (періодичні). Моментним називається ряд динаміки, величини якого характеризують стан явища на певний момент часу (на початок місяця, кварталу, року і т. ін.). Серед моментних показників можна назвати кількість населення, парк автомобілів і тракторів, поголів'я худоби тощо.
Ряд динаміки, величини якого характеризують розміри суспільних явищ за певні періоди (інтервали), називається інтервальним. Цей ряд характеризує процеси, які відбулися за певний період часу – добу, декаду, місяць, квартал, рік і т. ін. До таких показників належать обсяг виробленої продукції, витрати виробництва, фонд заробітної плати тощо.
Прикладом інтервальних рядів можуть бути дані табл. 10.18, які характеризують виробництво окремих видів продукції добувної промисловості за кожен рік.
Таблиця 10.18. Виробництво окремих видів продукції добувної промисловості в Україні за 2000–2005 pp., млн т
Вид продукції | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
Вугілля готове | 62,4 | 61,7 | 59,5 | 59,8 | 59,4 | 60,4 |
Торф неагломерований паливний | 0,4 | 0,3 | 0,5 | 0,6 | 0,5 | 0,6 |
Нафта, включаючи газовий конденсат | 3,7 | 3,7 | 3,7 | 4,0 | 4,3 | 4,4 |
Газ натуральний, млрд м8 | 17,9 | 18,4 | 18,7 | 19,3 | 20,4 | 20,8 |
Руди і концентрати залізні неагломеровані | 55,9 | 55,3 | 59,4 | 63,0 | 66,0 | 69,5 |
Динамічні ряди наростаючих підсумків. Особливістю інтервал ьних рядів динаміки є те, що їх показники можна підсумовувати. Наприклад, місячні обсяги виробництва продукції можна скласти й одержати квартальні або річні. Саме на цій особливості ґрунтується спосіб визначення наростаючих підсумків, який часто використовується в економічному аналізі, зокрема при вивченні рівня та контролю виконання плану виробництва продукції, робіт і надання послуг.
Для побудови динамічного ряду наростаючих підсумків обчислюється процентне відношення кожного такого підсумку до завдання на весь плановий період. В результаті отримаємо ряд чисел, які характеризують хід виконання плану у відносних показниках. Наприклад, підприємство має виробити за планом на півроку 700 тис. грн, за місяцями такий обсяг продукції було вироблено (тис. грн):
Показник | Січень | Лютий | Березень | Квітень | Травень | Червень |
Обсяг виробництва | 67 | 75 | 82 | 93 | 118 | 154 |
Розрахуємо проценти виконання плану наростаючим підсумком з початку року:
– за січень план виконаний на 67: 700 ž 100 = 9,6 (%);
– за січень і лютий місяці на (67 + 75): 700 ž 100 = 20,3 (%.);
– за січень-березень на (67 + 75 + 82): 700 ž 100 = 32,0 (%);
– за січень-квітень на (67 + 75 + 82 + 93) : 700 ž 100 = 45,3 (%);
– за січень-травень на (67 + 75 + 82 + 93 + 118) : 700 ž100 = 62,1 (%);
– за січень-червень на (67 + 75 + 82 + 93 + 118 + 154) : 700 ž 100 = 84,1 (%).
Побудова ряду динаміки вимагає дотримання таких вимог: 1. Всі показники ряду динаміки мають бути точними, вірогідними, науково обґрунтованими. У разі недотримання цієї вимоги можуть бути зроблені помилкові висновки.
2. Показники ряду динаміки мають бути порівнянні. Для цього необхідно, щоб склад досліджуваної сукупності був одним і тим самим в усьому ряду, тобто за:
– методологією розрахунків;
– територією;
– часом;
– колом охоплюваних об'єктів.
Порівнянність показників динаміки за методологією розрахунків досягається шляхом використання єдиних методологічних підходів. Так, виробництво валової продукції подається в єдиних порівняльних цінах.
Порівнянність показників динаміки за територією передбачає незмінність територіальних меж об'єктів дослідження.
Для перетворення незіставних рядів у зіставні роблять перерахунок даних за допомогою різних прийомів, насамперед шляхом прямого перерахунку даних. Наприклад, у випадках, коли територіальні межі змінилися (укрупнення території адміністративного району за рахунок приєднання частини земель сусіднього району), при побудові ряду динаміки чисельності населення за попередні роки слід зробити поправку на приєднану територію, тобто збільшити цю чисельність населення на кількість проживаючих в той же період на території, що пізніше була приєднана.
Порівнянність показників динаміки у часі означає, що ці показники мають бути обчислені за однакові періоди часу або на одну й ту саму дату. За відсутності необхідних даних робляться відповідні перерахунки. Наприклад, не можна будувати ряд динаміки обсягу роздрібного товарообороту за 1997– 2007 рр., якщо є інформація тільки за 1997–2006 рр., а за 2007 р. – тільки за 9 місяців. У такому випадку беруться дані кожного року за 9 місяців або будують ряд після закінчення 2007 р.
Порівнянність рядів динаміки за колом охоплюваних ними об'єктів (наприклад, малих підприємств) потребує дотримання однакової кількості досліджуваних об'єктів. Наприклад, якщо до 2005 р. в місті налічувалося 1260 підприємств малого бізнесу, а потім ще зареєструвалося 75, то при побудові ряду динаміки за 2004–2007 pp. необхідно всі показники обирати, виходячи зі складу малих підприємств до 2004 р., тобто по 1260 підприємствах.
Крім того, необхідно, щоб дані динамічного ряду були виражені в одних і тих самих одиницях виміру. Зокрема, не можна показувати в одному ряду обсяги виробництва молока чи реалізації пального в літрах, кілограмах чи тоннах.
До того ж проміжки часу між значеннями ряду мають бути за можливості однаковими. Не допускається також поєднання в одному ряду динаміки періодів і моментів часу. Так, не можна порівнювати середньорічну чисельність працівників на підприємстві з їх чисельністю на початок року.
Проведення економічного аналізу вимагає тривалого періоду спостереження і достатньої кількості показників ряду. Це пояснюється тим, що іноді тенденція розвитку не помітна чітко і тоді слід збільшити кількість періодів (моментів) спостереження (років, місяців, дат тощо). Вважається, що аналіз доцільно проводити за період у три – п'ять років, а при вивченні тенденцій слід брати не менше п'яти років. У випадку, коли необхідні дані відсутні, динамічний ряд потрібно вирівняти.
Основні показники аналізу динамічних рядів. Для аналізу рядів динаміки використовується ряд показників, які характеризують напрям, інтенсивність змін досліджуваних явищ та процесів. До них належать рівень ряду, середній рівень, абсолютний приріст, темп зростання, темп приросту, абсолютне значення одного процента приросту.
Розрахунок цих показників проводять шляхом порівняння між собою рівнів ряду динаміки. При цьому необхідно правильно вибирати базу порівняння, яка залежить від мети дослідження. При порівнянні кожного рівня з попереднім отримуємо ланцюгові показники. Якщо всі рівні зіставляються з одним і тим самим постійним рівнем (базою), то такі показники називаються базисними.
Рівень ряду – це кожен член ряду динаміки. Перший показник ряду є початковим рівнем, а останній – кінцевим.
Рівень ряду дає узагальнену характеристику рядам динаміки. Проте він не дозволяє визначити напрям і розмір змін рівнів ряду у часі. Для вирішення цього завдання необхідно застосувати аналітичні показники ряду динаміки: абсолютний приріст, темп зростання, темп приросту, абсолютне значення 1% приросту.
Приклад. Зробити аналіз динаміки обсягу виданих короткострокових кредитів за 1999–2007 pp. Для зручності і наочності вихідні і розрахункові показники викладемо у табличній формі (табл. 10.19).
Для вираження абсолютної швидкості зростання (зниження) рівнів ряду динаміки обчислюють показник абсолютний приріст (А). Величина його визначається як різниця між даним рівнем і рівнем, з яким проводиться зіставлення. Абсолютний приріст показує, на скільки одиниць підвищився або зменшився рівень ряду порівняно з базисним рівнем. Він розраховується за формулою
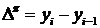 – абсолютний приріст ланцюговий
– абсолютний приріст ланцюговий
або
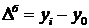 – абсолютний приріст базисний,
– абсолютний приріст базисний,
де 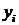 – рівень і-го року;
– рівень і-го року; 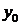 – рівень базисного року.
– рівень базисного року.
Інтенсивність зміни рівнів ряду динаміки оцінюється за допомогою такого показника, як темп зростання (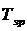 ). Він становить відношення поточного рівня до попереднього (
). Він становить відношення поточного рівня до попереднього (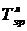 ) або базисного (
) або базисного (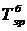 ).
).
Цей показник здебільшого виражається у процентах, тобто
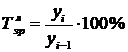 або
або 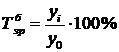
Темп зростання може виражатися і в коефіцієнтах. Тоді він показує, у скільки разів даний рівень ряду більший (менший) від рівня базисного року або яку частину його він становить.
Для виявлення змін величини абсолютного приросту рівнів ряду динаміки у відносних величинах визначається темп приросту (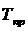 ). Він є відношенням абсолютного приросту до попереднього або базисного рівня
). Він є відношенням абсолютного приросту до попереднього або базисного рівня
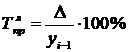 або
або 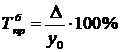
Зручним способом розрахунку темпу приросту є визначення його як різниці між темпом приросту та 100%, тобто
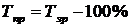 .
.
Рік | Сума виданих кредитів, млн грн | Абсолютний приріст (зниження), млн грн | Темп зростання,% | Темп приросту,% | Абсолютне значення 1% приросту, млн грн | |||
ланцюговий | базисний | ланцюговий | базисний | ланцюговий | базисний | |||
1999 | 104,7 | – | 0,0 | – | 1,0 | – | 0,0 | – |
2000 | 102,5 | -2,2 | -2,2 | 97,9 | 97,9 | -2,1 | -2,1 | ІД |
2001 | 261,4 | 158,9 | 156,7 | 255,0 | 249,7 | 155,0 | 149,7 | 1,0 |
2002 | 327,3 | 65,9 | 222,6 | 125,2 | 312,6 | 25,2 | 212,6 | 2,6 |
2003 | 354,9 | 27,6 | 250,2 | 108,4 | 339,0 | 8,4 | 239,0 | 3,3 |
2004 | 377,4 | 22,5 | 272,7 | 106,3 | 360,5 | 6,3 | 260,5 | 3,6 |
2005 | 402,8 | 25,4 | 298,1 | 106,7 | 384,7 | 6,7 | 284,7 | 3,8 |
2006 | 422,3 | 19,5 | 317,6 | 104,8 | 403,3 | 4,8 | 303,3 | 4,0 |
2007 | 444,4 | 22,1 | 339,7 | 105,2 | 424,5 | 5,2 | 324,5 | 4,2 |
Темп приросту свідчить про те, на скільки процентів даний рівень ряду більший (менший) від рівня попереднього чи базисного рівня ряду.
Абсолютне значення одного процента приросту (Д%) визначається як результат ділення абсолютного приросту на відповідний темп приросту, виражений у процентах. Розрахунок цього показника має економічний зміст тільки на ланцюговій основі.
У проведенні аналітичних досліджень особливу увагу слід приділяти методам розрахунку середніх величин рядів динаміки. Вони виступають узагальнюючою характеристикою його абсолютних рівнів, абсолютної швидкості та інтенсивності змін рівнів ряду динаміки. Розрізняють такі середні показники: середній рівень ряду динаміки, середній абсолютний приріст, середній темп зростання та приросту.
Методи розрахунку середнього рівня ряду динаміки залежать від його виду і способу отримання даних. Так, для інтервальних рядів середня розраховується за формулою середньої арифметичної, причому з рівновіддаленими рівнями за часом – середньої арифметичної простої
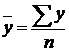 ,
,
а при нерівно віддалених – середньої арифметичної зваженої
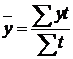 ,
,
де t – число часових періодів, протягом яких рівень не змінюється.
У нашому прикладі середня сума виданих короткострокових кредитів склала:
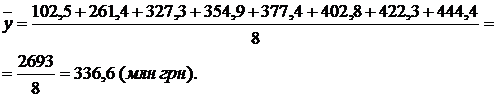
Середні значення моментного ряду з рівними інтервалами визначаються за допомогою середньої хронологічної. Якщо інтервали між періодами нерівні, то застосовується середня арифметична зважена, де в ролі ваг беруться відрізки часу між датами, до яких належать парні середні суміжних значень рівня.
Визначення середнього абсолютного приросту здійснюється за ланцюговими абсолютними приростами за формулою
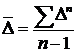 , або
, або 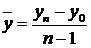 ,
,
Середньорічний абсолютний приріст суми виданих короткострокових кредитів за 1999-2007 pp. дорівнює
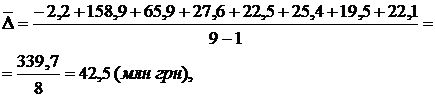
або
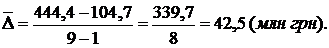
Середній темп зростання обчислюється за формулою середньої геометричної:
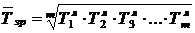 , або
, або 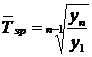 ,
,
де m – число коефіцієнтів зростання, n – число рівнів ряду динаміки.
Середньорічний темп зростання виплат короткострокових кредитів за 1999-2007 pp. розрахований двома способами:
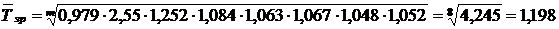 ,
,
або 119,8%,
чи 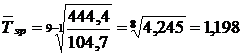 , або 119,8%.
, або 119,8%.
Середньорічний темп приросту отримаємо, віднімаючи від середнього темпу зростання 100%:
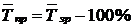 .
.
Так, у нашому прикладі цей показник дорівнює
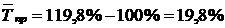
Прийоми обробки та аналізу рядів динаміки. Характерною особливістю рядів динаміки є постійна зміна, коливання їх рівнів, зумовлені дією як об'єктивних (сезонність, зміна умов виробництва тощо), так і випадкових чинників (форс-мажорні обставини та ін.). Залежно від цього завдання аналітика полягає у забезпеченні порівнянності рівнів ряду, виявленні основних тенденцій, закономірностей розвитку явища за певні періоди часу без врахування дії випадкових факторів. У свою чергу такий підхід створить підґрунтя для прогнозування динаміки досліджуваного явища у майбутньому, що має важливе значення в управлінні виробництвом.
У зв'язку з цим ряди динаміки потребують певної обробки за допомогою таких прийомів, як змикання рядів, приведення їх до однієї основи, вирівнювання тощо.
Змикання динамічних рядів. Цей прийом обробки рядів динаміки застосовується тоді, коли у процесі аналізу виявлено непорівнянність рівнів ряду за одні роки (чи інші періоди) з рівнями за інші роки через територіальні, відомчі чи організаційні зміни, застосування різної методології обчислення показників, показників виміру та ін. Є кілька способів приведення рядів динаміки до порівнянного вигляду.
Приклад. Є дані про виробництво валової продукції групи підприємств однієї із галузей (табл. 10.20). Привести ряд динаміки до зіставного виду.
Для приведення ряду динаміки до зіставного виду необхідно визначити для 2003 р. коефіцієнт співвідношення рівнів двох рядів: 45,6 : 42,4 = 1,08.
Перемноживши на цей коефіцієнт рівні першого ряду, отримаємо їх порівнянність з рівнями другого ряду:
2000 р. – 38,2 ž 1,08 " 41,3 млн грн;
2001 р. – 39,4 ž 1,08 - 42,6 млн грн;
2002 р. – 40,0 ž 1,08 = 43,2 млн грн.
Таблиця 10.20. Динаміка виробництва валової продукції групи підприємств в області за 2000-2007 pp., у порівняльних цінах 2000 р., млн грн
Показник | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
Обсяг валової продукції: | ||||||||
у старих межах області | 38,2 | 39,4 | 40,0 | 42,4 | – | – | ||
у нових межах | – | – | – | 45,6 | 47,2 | 49,0 | 52,4 | 56,2 |
Отриманий зіставний ряд динаміки валової продукції групи підприємств однієї з областей в нових межах:
Рік | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
Млн грн | 41,3 | 42,6 | 43,2 | 45,6 | 47,2 | 49,0 | 52,4 | 56,2 |
За даними такого ряду розраховують темпи зростання і приросту щодо будь-якого року. Так, обсяг валової продукції у 2007 р. становив 56,2 млн грн, або 136,1% щодо 2000 p., тобто збільшився приблизно в 1,36 разу, або на 36,1%.
Інший спосіб змикання рядів динаміки полягає в тому, що рівні року, в якому відбулися зміни (у нашому прикладі 2003 p.), як до змін, так і після них (для нашого прикладу в старих і нових межах, тобто 42,4 і 45,6) приймаються за 100%, а інші – перераховуються у процентах щодо цих рівнів відповідно (у нашому прикладі до змін – щодо 42,4, а після змін – щодо 45,6). В результаті вийде зімкнутий ряд:
Рік | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
Валова продукція в нових межах області, в% до 2003 р. | 90,1 | 92,9 | 94,3 | 100,0 | 103,5 | 107,5 | 114,9 | 123,2 |
Приведення рядів динаміки до однієї основи. У проведенні аналітичних досліджень часто виникає необхідність порівняти між собою кілька споріднених показників або взаємопов'язаних явищ (наприклад, обсяг виробництва різних видів продукції) за ряд років. Це успішно можна зробити за допомогою способу приведення рядів динаміки до однієї основи. Сутність його полягає у переведенні абсолютних показників ряду у відносні, взявши при цьому якийсь період (рік, місяць і т. п.) за одиницю, або 100 (основа ряду). Як правило, базою порівняння вибирають той рівень року, який має певне економічне чи історичне значення для розвитку досліджуваного явища.
Розглянемо цей спосіб на прикладі даних табл. 10.21.
Таблиця 10.21. Динаміка середньомісячної номінальної заробітної плати найманих працівників в Україні, грн
Рік | Номінальна зарплата, всього | У тому числі | ||||
у промисловості | у сільському господарстві, мисливстві та лісовому господарстві | |||||
грн | У% до 2000 р. | грн | У% до 2000 р. | грн | У% до 2000 р. | |
2000 | 230 | 100,0 | 302 | 100,0 | 114 | 100,0 |
2001 | 311 | 135,2 | 406 | 134,4 | 154 | 135,1 |
2002 | 376 | 163,5 | 485 | 160,6 | 183 | 160,5 |
2003 | 462 | 200,9 | 591 | 195,7 | 219 | 192,1 |
2004 | 590 | 256,5 | 743 | 246,0 | 311 | 272,8 |
2005 | 806 | 350,4 | 967 | 320,2 | 437 | 383,3 |
За основу, чи базу порівняння прийнято абсолютний рівень 2000 р. Як бачимо, темпи зростання зарплати найманих працівників у суспільному господарстві за 2000–2005 pp. були наближені до темпів зростання її в промисловості і сільському господарстві, мисливстві і лісовому господарстві.
Виявлення основної тенденції ряду динаміки. Найважливішим завданням аналізу рядів динаміки є виявлення закономірностей розвитку явища, а саме загальної тенденції динаміки та її характеру (типу).
Загальна тенденція динаміки означає напрям розвитку (схильність, спрямування) до зростання, стабільності або зниження рівня певного явища. Характер (тип) динаміки – це та чи інша тенденція зміни аналітичних показників динаміки (абсолютного приросту, темпу зростання чи темпу приросту).
Характер динаміки розглянемо на прикладі зміни врожайності окремих сільськогосподарських культур у господарстві за вісім років (табл. 10.22).
Наведені в таблиці дані відображають загальну тенденцію зростання врожайності всіх трьох видів сільськогосподарських культур. Водночас спостерігається неоднаковий характер такого зростання. Так, абсолютні прирости врожайності картоплі відносно стабільні, а темпи приросту свідчать про тенденцію до деякого зниження.
Показники врожайності цукрових буряків мають інший характер: абсолютні прирости їх збільшуються щорічно, а темпи зростання стабілізувалися на рівні 16–18%. Урожайність же ярого ячменю прискорено зростає.
Отже, зростання рівнів ряду динаміки може здійснюватися з різною інтенсивністю, а завдання аналізу полягає у встановленні загальних тенденцій, характеру змін для досліджуваного періоду.
В економічному аналізі виділяються такі основні типи форм характеру динаміки:
– І – абсолютні прирости знижуються (зі збільшенням рівнів ряду абсолютний приріст і темпи зростання знижуються);
– II – абсолютні прирости стабільні (зростання рівнів ряду супроводжується стабільністю абсолютних приростів та зниженням темпів приросту);
– III – темпи зростання стабільні (абсолютні прирости збільшуються при стабільних темпах зростання);
– IV – темпи зростання збільшуються (інтенсивне підвищення рівнів ряду при постійному збільшенні темпів зростання).
Отже, незважаючи на постійне зростання рівнів ряду динаміки, характеристика її розвитку, як свідчать вищеназвані типи, різна.
Таблиця 10.22. Динаміка врожайності сільськогосподарських культур у господарстві за 2000-2007 pp.
Рік | Картопля | Цукровий буряк | Ячмінь яровий | ||||||
Урожайність, ц/га | Приріст ланцюговий | Урожайність, ц/га | Приріст ланцюговий | Урожайність, ц/га | Приріст ланцюговий | ||||
абсолютний, Ц | темп приросту,% | абсолютний, ц | темп приросту,% | абсолютний, Ц | темп приросту,% | ||||
2000 | 93,4 | – | – | 169,0 | – | – | 14,4 | – | – |
2001 | 112,2 | 18,8 | 20,1 | 197,7 | 28,7 | 17,0 | 15,0 | 0,6 | 4,2 |
2002 | 132,0 | 19,8 | 17,6 | 237,1 | 39,4 | 19,9 | 16,5 | 1,5 | 10,0 |
2003 | 154,0 | 22,0 | 16,7 | 279,8 | 42,7 | 18,0 | 18,7 | 2,2 | 13,3 |
2004 | 176,0 | 22,0 | 14,3 | 324,5 | 44,7 | 16,0 | 21,6 | 2,9 | 15,5 |
2005 | 195,8 | 19,8 | 11,3 | 383,4 | 58,9 | 18,2 | 27,8 | 6,2 | 28,7 |
2006 | 216,7 | 20,9 | 10,7 | 443,8 | 60,4 | 15,8 | 34,1 | 6,3 | 22,7 |
2007 | 236,0 | 19,3 | 8,9 | 516,5 | 72,7 | 16,4 | 40,5 | 6,4 | 18,8 |
На практиці не завжди вдається одразу виявити загальну тенденцію розвитку і характер динаміки за допомогою ланцюгових показників. Це пояснюється тим, що рівні ряду і розраховані на їх основі ланцюгові показники можуть значно коливатися (варіювати) за роками у той чи інший бік (зниження, підвищення). У таких випадках основна закономірність, тенденція розвитку явища, ніби розмивається. Для її виявлення доцільно застосовувати такі прийоми, як згладжування (вирівнювання) рівнів ряду шляхом укрупнення інтервалів або ковзної (рухомої) середньої.
Згладжування (вирівнювання) рівнів ряду шляхом укрупнення інтервалів – один із найбільш поширених простих способів виявлення закономірності зміни рівнів динаміки за допомогою розрахунку середніх або підсумкових показників з метою укрупнення періодів (інтервалів) часу.
Розглянемо динаміку врожайності озимої пшениці в господарстві за 12 років (табл. 10.23).
Таблиця 10.23. Динаміка врожайності озимої пшениці у господарстві за 1996-2007 pp.
Рік | Урожайність, ц/га | Сумарна врожайність за 3 роки, ц | Середня врожайність за 3 роки, ц/га |
1996 | 16,5 | 54,9 | 18,3 |
1997 | 17,6 | ||
1998 | 20,8 | ||
1999 | 17,4 | 61,0 | 20,3 |
2000 | 22,1 | ||
2001 | 21,5 | ||
2002 | 21,9 | 67,2 | 22,4 |
2003 | 23,5 | ||
2004 | 21,8 | ||
2005 | 29,9 | 87,4 | 29,1 |
2006 | 26,5 | ||
2007 | 31,0 |
У результаті проведено укрупнення періодів, тенденція зростання врожайності озимої пшениці виявляється чіткіше.
Такій обробці доцільно піддавати динамічний ряд з більш-менш постійними коливаннями рівня. Укрупнення періодів і аналіз їх за допомогою середніх величин сприяє виявленню виразної тенденції зміни явища у часі. При укрупненні інтервалів важливо правильно вибрати довжину періоду, за яким проводиться укрупнення (три, чотири, п'ять і т. п. років, місяців, днів).
Згладжування способом ковзної середньої – спосіб виявлення загальної тенденції динамічного ряду, сутність якого полягає в укрупненні періодів шляхом послідовних зрушень на одну дату (рік, місяць, тиждень) при збереженні постійного інтервалу періоду (три, п'ять років тощо).
Назва ковзної середньої пояснюється тим, що вона розраховується, ніби ковзаючи по ряду динаміки від його початку до кінця, відкидаючи при цьому один рівень з початку і додаючи наступний.
Приклад. На основі даних про врожайність озимої пшениці господарства за 12 років здійснити згладжування ряду методом трирічної ковзної середньої.
Порядок обчислення змінної (ковзної) середньої відображено в табл. 10.24.
Таблиця 10.24. Розрахунок трирічної ковзної середньої врожайності озимої пшениці у господарстві за 1996-2007 pp.
Рік | Врожайність, ц/га | Сума врожайності за 3 роки, ц | Ковзна середня, ц/га |
1 | 2 | 3 | 4 |
1996 | 16,5 | – | – |
1997 | 17,6 | – | 18,3 |
1998 | 20,8 | 54,9 | 18,6 |
1999 | 17,4 | 55,8 | 20,1 |
2000 | 22,1 | 60,3 | 20,3 |
2001 | 21,5 | 61,0 | 21,8 |
2002 | 21,9 | 65,5 | 22,3 |
2003 | 23,5 | 66,9 | 22,4 |
2004 | 21,8 | 67,2 | 25,1 |
2005 | 29,9 | 75,2 | 26,1 |
2006 | 26,5 | 78,2 | 29,1 |
2007 | 31,0 | 87,4 | – |
Взявши дані за перші три роки, обчислюємо трирічні суми, а потім середню врожайність:
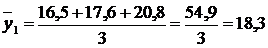 ;
;
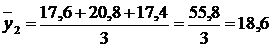 і т.п.
і т.п.
Слід врахувати, що кожна ланка ковзної середньої умовно відноситься (записується або наноситься на графік) до середини відповідного періоду.
Отже, як видно з таблиці, після згладжування ряду динаміки врожайності озимої пшениці за допомогою трирічної ковзної чітко простежується тенденція до зростання врожайності. Крім цього, завдяки згладжуванню можна детальніше ніж при укрупненні інтервалів дослідити і характер розвитку. Зокрема, вихідні показники врожайності свідчать, що зростання її відбувалося нерівномірно. За допомогою згладжування вдалося вирівняти цю нерівномірність, зменшивши при цьому вплив річних відхилень (метеорологічних умов тощо).
Незважаючи на важливість, спосіб ковзної середньої має і певний недолік, який полягає у тому, що згладжений ряд укорочується порівняно з фактичним. Це звужує інформаційну базу аналізу, може ускладнювати виявлення характеру динаміки.
Аналітичне вирівнювання – найефективніший спосіб обробки ряду динаміки з метою виявлення основної тенденції розвитку явища. Сутність його полягає у вирівнюванні фактичних даних динамічного ряду способом найменших квадраті в, що передбачає знаходження такої прямої або кривої, ординати точок якої були б найближчі до значень фактичного ряду динаміки.
Найпростішою лінією, яка використовується при вирівнюванні ряду динаміки, є пряма. Вона використовується тоді, коли швидкість зростання, приросту або абсолютних відхилень явища потягом досліджуваного періоду відбувається більш-менш рівномірно. При такому вирівнюванні завдяки усуненню впливу випадкових факторів досліджуване явище змінюватиметься щороку на одну й ту саму величину в арифметичній прогресії.
Рівняння прямої має такий вигляд:
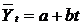 ,
,
де 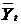 – вирівняне значення членів динамічного ряду;
– вирівняне значення членів динамічного ряду;
a, b – параметри прямої;
t – відрізки або моменти часу (порядковий номер року, який набуває значення 1, 2, 3 і т. д.).
Параметри рівняння знаходять шляхом складання і розв'язання так званих нормальних рівнянь:
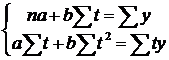
де n – кількість років у періоді, що вивчається.
Цю систему рівнянь можна значно спростити, якщо відлік часу брати з середини ряду, умовно взятого за нуль. Тоді слід зазначити, що 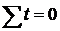 . При непарній кількості рівнів ряду значення t встановлюється так, як показано в наведеному нижче прикладі.
. При непарній кількості рівнів ряду значення t встановлюється так, як показано в наведеному нижче прикладі.
Приклад. Наведені нижче дані характеризують динаміку кількості працівників промислових підприємств області, які підвищили свою кваліфікацію у 2003-2007 pp.:
Рік | 2003 | 2004 | 2005 | 2006 | 2007 |
Кількість працівників, осіб | 2074 | 2030 | 2164 | 2339 | 2502 |
Визначити тенденцію зміни рівнів ряду динаміки способом аналітичного вирівнювання.
З метою визначення основної тенденції зміни чисельності працівників промислових підприємств області, які підвищили свою кваліфікацію, доцільно використати метод аналітичного вирівнювання. У цій задачі абсолютні прирости більш-менш постійні, рівні ряду змінюються близько до арифметичної прогресії, тому вирівнювання зробимо за прямою за допомогою складання рівняння у вигляді лінійної функції типу
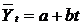 .
.
Для визначення параметрів рівняння складемо спрощену систему рівнянь. Початок відліку часу (t = 0) перенесемо на середину динамічного ряду (табл. 10.25).
Таблиця 10.25. Розрахункові дані для визначення параметрів трендової лінії кількості працівників
Рік | Кількість працівників, осіб, у | t | t2 | yt | Теоретичне значення, |
2003 | 2 074 | -2 | 4 | -4 148 | 1 988,8 |
2004 | 2 030 | -1 | 1 | -2 030 | 2 105,3 |
2005 | 2164 | 0 | 0 | 0 | 2 221,8 |
2006 | 2 339 | 1 | 1 | 2 339 | 2 338,3 |
2007 | 2 502 | 2 | 4 | 5 004 | 2 454,8 |
Разом | 11109 | 0 | 10 | 1165 | 11109 |
Система рівнянь матиме такий вигляд:
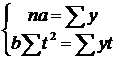
Із таблиці 10.25 знаходимо
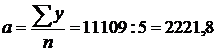 ;
;
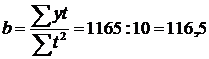 .
.
Знайдені значення параметрів а і b дають можливість побудувати рівняння прямої:
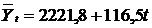 .
.
Отже, як свідчать вирівняні рівні часового ряду за 2003-2007 рр., величина 2221,8 (заокруглено 2222 особи) показує теоретичну кількість працівників промислових підприємств області, які підвищили свою кваліфікацію у 2005 р., для якого ми взяли нульовий номер року, а величина b = 116,5 (заокруглено 117 осіб) показує середню величину приросту числа працівників за рік.
Підставляючи у рівняння по черзі значення t, одержимо вирівняний (теоретичний) динамічний ряд кількості працівників промислових підприємств області, які підвищили свою кваліфікацію.
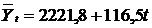
Причому цей ряд абстрагований від випадкових коливань і характеризується систематичним збільшенням. Значення у і 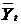 зображені та графіку (рис. 10.2).
зображені та графіку (рис. 10.2).
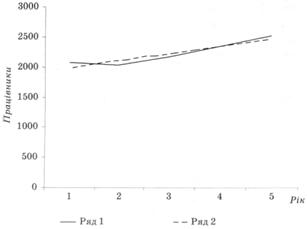
Рис. 10.2. Фактична і вирівняна кількість працівників, які підвищили кваліфікацію, осіб
При парній кількості років, наприклад шість років, – значення t можуть мати такий вигляд: -3; -2; -1; +1; +2; +3 (зверху вниз).
Крім прямої лінії, яку ми детально розглянули, при вирівнюванні ряду динаміки можуть використовуватися також парабола другого порядку (коли абсолютні прирости рівномірно збільшуються і при згладжуванні крива має один вигин), парабола третього порядку (якщо криві при згладжуванні мають два вигини), показова функція (коли ряд динаміки відображає розвиток у геометричній прогресії) та ін. Вирівнювання рядів динаміки за цими та іншими типами аналітичних функцій здійснюється в аналогічній послідовності, як було показано вище.
Вимірювання сезонних коливань. В дослідженні сезонних коливань велику роль відіграють ряди динаміки, особливо в тих видах економічної діяльності, які мають сезонний характер (сільське господарство, будівництво та ін.). При цьому застосовують різні прийоми, найбільш поширеним серед яких є обчислення відхилень внутрішньорічних даних використовуючи середньорічні.
Приклад. Проаналізувати сезонність виробництва молока за такими даними (табл. 10.26).
Сезонність характеризується відношенням кожного рівня до середнього рівня ряду динаміки. Послідовність проведення розрахунків така:
1. Визначення середнього рівня ряду, тобто середньомісячного надою молока за формулою середньої арифметичної простої:
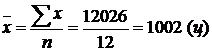 ,
,
де 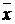 – середній рівень;
– середній рівень;
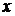 – рівень кожного місяця;
– рівень кожного місяця;
N – число місяців.
2. Розрахунок показників сезонності – відношення щомісячного надою до середнього надою 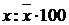 .
.
Таблиця 10.26. Валовий надій молока в сільськогосподарському підприємстві за місяцями року
Місяць | Валовий надій, ц | Показники сезонності (рівень кожного місяця в% до середньомісячного рівня) |
|
| |
Січень | 801 | 79,9 |
Лютий | 982 | 98,0 |
Березень | 1002 | 100,0 |
Квітень | 1014 | 101,2 |
Травень | 1 197 | 119,5 |
Червень | 1590 | 158,7 |
Липень | 1 120 | 111,8 |
Серпень | 1 189 | 118,7 |
Вересень | 944 | 94,2 |
Жовтень | 773 | 77,1 |
Листопад | 700 | 69,9 |
Грудень | 714 | 71,3 |
Разом | 12026 | – |
Розраховані показники сезонних коливань молока показують, що надій молока в літні та весняні місяці значно збільшується, а в зимові та осінні – зменшується. Так, у червні валовий надій молока в господарстві становить 1590 ц, що майже в 1,6 разу перевищує середньомісячний рівень цього показника.
10.6. Балансовий метод
10.7. Метод деталізації
10.8. Порівняння
10.9. Методи порівняльної комплексної оцінки
НАВЧАЛЬНИЙ ТРЕНІНГ
Розділ 11. МЕТОДИ ДЕТЕРМІНОВАНОГО ФАКТОРНОГО АНАЛІЗУ
11.1. Індексний метод
11.2. Метод різниць
11.3. Інтегральний метод