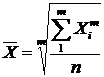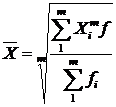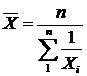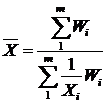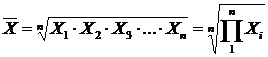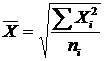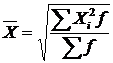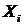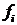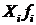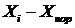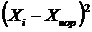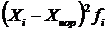Теорія економічного аналізу - Купалова Г.І. - 10.1.3. Середні величини

Усі явища і процеси суспільного та господарського життя характеризуються значною динамічністю. Наприклад, розмір середньомісячної заробітної плати робітників, собівартості одиниці продукції, обсяг виробництва й реалізації варіюють у широких межах всередині підприємства та поза його межами в різні періоди, за різними видами економічної діяльності. Природно, що для узагальнення та різнобічного аналізу даних необхідно розрахувати середні величини досліджуваної сукупності за соціальними та професійними групами, виробничими підрозділами, підприємствами і видами діяльності, за адміністративними районами, областями, по Україні в цілому тощо. Під середньою величиною розуміють узагальнюючий показник, який характеризує типовий рівень варіюючої ознаки в розрахунку на одиницю однорідної сукупності.

Усереднені показники мають важливе наукове та практичне значення в управлінні економікою, для планування, прогнозування, моніторингу, контролю на рівні окремих господарських та адміністративних одиниць, а також країни. Порівняння середніх показників у часі, просторі, з планом дасть змогу здійснити глибокий, обґрунтований аналіз досліджуваних явищ, зокрема охарактеризувати досягнутий об'єктивний рівень розвитку і місце на ринку окремих підприємств та відомств, працівників. Це сприяє виявленню суспільних, економічних закономірностей, які проявляються в конкретних умовах місця і часу.

Наприклад, є певна залежність між енергозабезпеченістю та енергоозброєністю сільськогосподарської праці – чим більше енергетичних потужностей припадає на 100 га посівів, тим менша (за інших рівних умов) потреба у працівниках. Тому енергоозброєність праці зростає швидше, ніж енергозабезпеченість. Аналогічно можна порівняти середні показники продуктивності праці та її оплати за останні десять років, що дасть можливість побачити розвиток досліджуваних явищ за цей період, у тому числі окремо продуктивності та оплати праці, а також порівняти їх відносні показники динаміки (коефіцієнти зростання), що характеризуватиме тенденцію до зростання чи зниження продуктивності плати щодо її оплати.

У практиці економічного аналізу виникають різноманітні завдання, мають місце особливості господарських процесів, які формують потребу у використанні того чи іншого виду середніх величин. Як відомо, всі види середніх величин виводять із формули степеневої середньої:

– простої

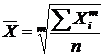
або

– зваженої

,

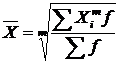де

m = 1 – середня арифметична;

m = 0 – середня геометрична;

m = –1 – середня гармонічна;

m = 2 – середня квадратична.

Отже, є такі основні види середніх величин: арифметична, гармонічна, квадратична, геометрична, хронологічна. Види та формули розрахунку середніх величин наведені в табл. 10.5.

Таблиця 10.5. Види та формули розрахунку середніх величин

Найбільш поширеним видом середніх величин є середня арифметична. Вона розраховується у тих випадках, коли обсяг осередненої ознаки утворюється як сума її окремих значень в окремих одиницях досліджуваної сукупності. Залежно від характеру вихідних даних середня арифметична визначається як середня арифметична проста – коли вихідні дані не згруповані, або як середня арифметична зважена – якщо дані розбиті на групи.

Примітки: х – степенева середня, рівень ознаки-варіант; 1 : х – зворотне значення варіанта; n – число варіантів або членів моментного ряду динаміки; т – обсяг сукупності; f – частоти; W – добуток варіанта на частоту; П – символ добутку.

Приклад. Необхідно розрахувати середньомісячну зарплату 10 робітників торговельного підприємства (у грн): 1700; 2000; 1500; 1300; 1300; 1500; 2000; 1500; 2000; 1500.

Використаємо формулу середньої арифметичної простої:

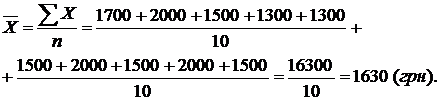
Згрупувавши ці дані за величиною ознаки і підрахувавши число випадків повторення кожної з них, отримаємо такий варіаційний ряд. Тоді середня арифметична зважена дорівнює (табл. 10.6)

Таблиця 10.6. Ряд розподілу працівників торговельного підприємства за розміром місячної заробітної плати

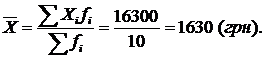
Середня гармонічна – це величина, обернена до середньої арифметичної. При цьому загальний обсяг значень ознаки утворюється як сума обернених значень ознаки.

Середня гармонічна проста використовується тоді, коли дані не згруповані, і обсяги явищ (добутки) за кожною ознакою рівні.

Приклад 1. Два робітники виготовили одну й ту саму кількість деталей. При цьому один виробляв 160 одиниць за годину, а другий – 180. Визначити середній виробіток робітників.

Розв'язання:

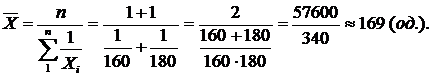
Середня гармонічна зважена використовується у тому випадку, коли дані розбиті на групи. Крім того, вихідна інформація не містить частот за окремими варіантами сукупності, а подана як добуток варіант на їх частоти.

Приклад 2. Розрахувати середню ціну реалізації картоплі на ринках трьох районів області, використовуючи дані табл. 10.7.

Таблиця 10.7. Ціна та сума реалізації картоплі на ринках районів

Розв'язання:

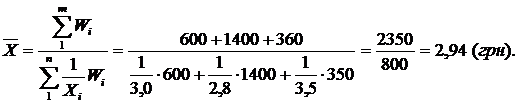
Середня геометрична використовується тоді, коли обсяг ознаки формується у вигляді добутку індивідуальних її значень, представлених відносними показниками. Найчастіше такими показниками виступають відносні показники динаміки (темп зростання).

Приклад. Кількість зареєстрованих малих підприємств за чотири роки зросла у 1,29 разу, у тому числі за перший рік – у 1,07, за другий – у 1,13, за третій – у 1,09, за четвертий скоротилася у 0,98 разу. Визначити середньорічний темп зростання кількості цих підприємств.

.

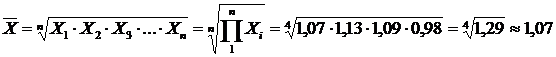Розв'язання:

Отже, середньорічний темп зростання кількості малих підприємств за чотири роки склав 1,07, або 107%.

При згрупованих даних у вигляді неоднакових часових інтервалів використовують середню геометричну зважену

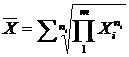
де х – значення ознаки за окремі періоди часу;

n_i – тривалість окремого періоду часу;

m – кількість періодів часу.

Середня квадратична застосовується у тому разі, коли обсяг значень ознаки утворюється як сума квадратів її окремих значень.

Середня квадратична буває проста (при незгрупованих даних)

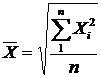
і зважена – коли дані розбиті на групи

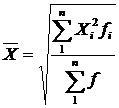
Наприклад, потрібно визначити середню сторону п'яти квадратів за умови, що їх площі становили: 25, 36, 64, 100 і 400 м². Тоді

.

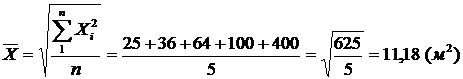Середня квадратична характеризує також варіацію. Тому на практиці вона використовується, коли варіанти ряду подані у вигляді відхилень фактичних їх значень від середньої арифметичної чи іншої величини, яка виступає у ролі норми чи нормативу, стандарту.

Середня квадратична проста

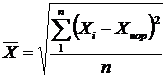
або середня квадратична зважена

.

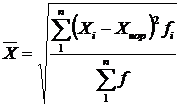Приклад. Обчислити середню величину відхилень фактичних показників виробництва запасних частин протягом місяця від встановлених норм (табл. 10.8).

Таблиця 10.8. Виробництво запасних частин за місяць

Використовуючи дані табл. 10.8, отримаємо такий результат

.

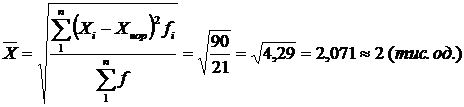Для вивчення економічних явищ і процесів у їх розвитку та зміні у часі використовують середні хронологічні величини. Вони призначені для отримання узагальнюючої характеристики динамічного ряду та його руху за той чи інший період часу.

Середня характеристика ряду динаміки обчислюється по-різному для інтервальних і моментних рядів динаміки, а також для відносних показників динаміки. Для інтервального ряду динаміки (відображає розміри явищ за певні проміжки часу) з рівними періодами середня хронологічна обчислюється за формулою середньої арифметичної простої, а з нерівними відрізками часу – середньої арифметичної зваженої.

Для моментного ряду динаміки (характеризує розміри економічних і суспільних явищ станом на якийсь момент, здебільшого на певну дату) середня хронологічна визначається по-іншому. Формула середньої хронологічної моментного ряду з рівними відрізками часу може бути записана так:

.

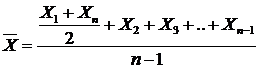Приклад. Розрахувати середню чисельність працівників підприємства за перший, другий квартали і півріччя, якщо на перше число кожного місяця працювала така кількість осіб:

– 1 січня – 122;

– 1 лютого – 145;

– 1 березня – 149;

– 1 квітня – 160;

– 1 травня – 158;

– 1 червня – 172;

– 1 липня – 170.

Розрахунок:

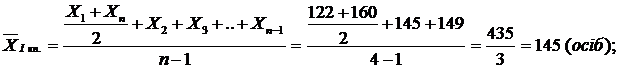
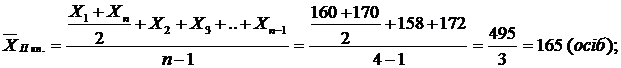
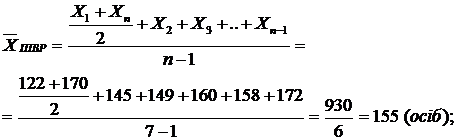
Для узагальнення відносних показників динаміки використовується середня геометрична, яка характеризує середній темп зміни рівнів ряду. Детальніше про цю середню подано в параграфі 10.4 "Побудова рядів динаміки".

Проте у проведенні аналітичних досліджень слід враховувати те, що всяка середня величина згладжує індивідуальні значення ознак, насамперед найнижчі та найвищі, найкращі та найгірші. Тому цілком прийнятне застосування середнього прогресивного показника, що розраховується з відповідних даних, вищих за середню величину сукупності.